介绍

在这个实验中，您将在 SimpleDB 的基础上实现一个查询优化器。主要任务包括实现一个选择性估算框架和一个基于成本的优化器。您在具体实现方面有一定的自由度，但我们建议使用类似于课堂上讨论的 Selinger 基于成本的优化器（第9讲）。

本文档的其余部分描述了添加优化器支持所涉及的内容，并提供了如何进行的基本概述。

与之前的实验一样，我们建议您尽早开始。

提示

  • 实现 TableStats 类中的方法，使其能够使用直方图（为 IntHistogram 类提供了框架）或您设计的其他形式的统计信息，估算过滤器的选择性和扫描成本。
  • 实现 JoinOptimizer 类中的方法，使其能够估算连接的成本和选择性。
  • 编写 JoinOptimizer 中的 orderJoins 方法。该方法必须针对一系列连接（可能使用 Selinger 算法），根据在前两个步骤中计算的统计信息生成最佳的连接顺序。

优化大纲

请记住，基于成本的优化器的主要思想是：

  • 利用关于表的统计信息来估算不同查询计划的“成本”。通常，计划的成本与中间连接和选择所产生的元组数量（基数），以及过滤和连接谓词的选择性相关。
  • 利用这些统计信息以最佳方式对连接和选择进行排序，并从多个备选的连接算法中选择最佳实现。 在这个实验中，您将实现代码来执行这两个功能。

优化器将从 simpledb/Parser.java 中调用。在开始本实验之前，您可能需要回顾一下实验 2 中的解析器练习。简而言之，如果你有一个描述表的目录文件 catalog.txt，你可以通过键入以下内容运行解析器

1
java -jar dist/simpledb.jar parser catalog.txt

调用解析器时，它将计算所有表的统计数据（使用您提供的统计代码）。当发出查询时，解析器会将查询转换为逻辑计划表示，然后调用查询优化器生成最优计划。

优化器结构

在开始实施之前，您需要了解 SimpleDB 优化器的整体结构。SimpleDB 模块的parser和optimizer的整体控制流程如图 1 所示。

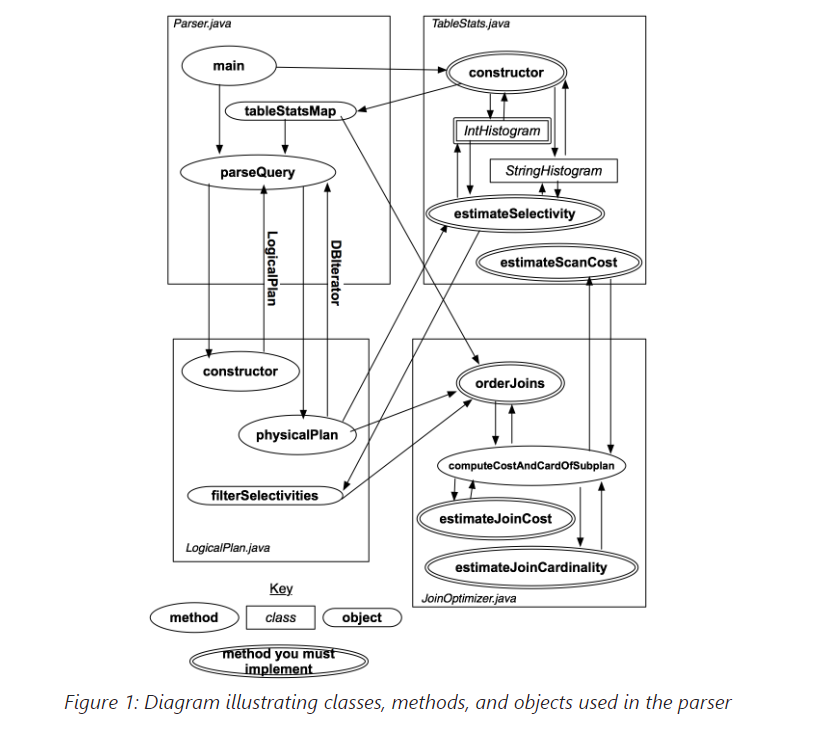
底部的键解释了这些符号；您将实现双边框的组件。在接下来的文本中，将更详细地解释类和方法（您可能希望参考这个图表），但基本操作如下：

  • 当Parser.java初始化时，它构造了一组表统计信息（存储在statsMap容器中）。然后，它等待输入查询，并在该查询上调用parseQuery方法。
  • parseQuery首先构造了一个表示解析查询的LogicalPlan。然后，parseQuery调用LogicalPlan实例上的physicalPlan方法。physicalPlan方法返回一个DBIterator对象，可用于实际运行查询。

在即将进行的练习中，您将实现帮助physicalPlan设计最佳计划的方法。

统计估算

准确估算计划成本是相当棘手的。在这个实验中，我们将仅关注连接顺序和基表访问的成本。我们不会考虑访问方法的选择（因为我们只有一种访问方法，即表扫描）或其他运算符（如聚合）的成本。

在这个实验中，您只需要考虑左深度计划。有关额外的“奖励”优化器功能的描述，请参见第2.3节，其中包括您可以实现的处理杂乱计划的方法。

整体计划成本

我们将会编写join计划，以如下的形式p=t1 join t2 join ... tn。它表示一个左深连接。其中t1是最左边的连接（树中最深的连接）。给定一个如p的计划，其成本可以表示为：

1
2
3
scancost(t1) + scancost(t2) + joincost(t1 join t2) +
scancost(t3) + joincost((t1 join t2) join t3) +
...

这里，scancost(t1)表示扫描表t1的I/O成本，joincost(t1, t2)表示将t1与t2连接的CPU成本。为了使I/O和CPU成本可比较，通常会使用一个常数缩放因子，例如：

1
2
cost(predicate application) = 1
cost(pageScan) = SCALING_FACTOR x cost(predicate application)

在这个实验中，您可以忽略缓存效应（例如，假设对表的每次访问都会产生完整的扫描成本）——同样，这是您可以在第2.3节中作为实验的可选奖励扩展添加的内容。因此，scancost(t1)简单地是t1中页面的数量 x SCALING_FACTOR。

连接成本

在使用嵌套循环连接时，请记住两个表 t1 和 t2（其中 t1 是外层表）之间的连接成本很简单：

1
2
joincost(t1 join t2) = scancost(t1) + ntups(t1) x scancost(t2) //IO cost
                       + ntups(t1) x ntups(t2)  //CPU cost

这里，ntups(t1)是表t1中的tuples数量。

过滤器的选择性

ntups 可以通过扫描基表直接计算。对于具有一个或多个选择谓词的表来估算 ntups 可能会更加棘手 — 这是过滤选择性估算的问题。以下是您可能采用的一种方法，基于在表中的值上计算直方图：

  • 计算表中每个属性的最小值和最大值（通过一次扫描实现）。

  • 为表中的每个属性构建直方图。一种简单的方法是使用固定数量的桶（NumB），每个桶代表直方图属性域中固定范围内的记录数量。例如，如果字段 f 范围从 1 到 100，且有 10 个桶，那么桶 1 可能包含记录数，其值在 1 到 10 之间，桶 2 包含记录数，在 11 到 20 之间，依此类推。

  • 再次扫描表，选择所有元组的所有字段，并使用它们来填充每个直方图的桶计数。

  • 要估算相等表达式 f=const 的选择性，请计算包含值 const 的桶。假设桶的宽度（值范围）为 w，高度（元组数量）为 h，表中的元组数量为 ntups。然后，假设值在整个桶中均匀分布，表达式的选择性大致为 (h / w) / ntups，因为 (h/w) 代表具有值 const 的桶中的预期元组数量。

  • 要估算范围表达式 f>const 的选择性，请计算包含 const 的桶 b，其宽度为 w_b，高度为 h_b。然后，b 包含总元组的分数 b_f = h_b / ntups。假设元组在 b 中均匀分布，则 b 中 > const 的部分 b_part 为 (b_right - const) / w_b，其中 b_right 是 b 桶的右端点。因此，桶 b 对谓词贡献了 (b_f x b_part) 的选择性。此外，桶 b+1…NumB-1 贡献了它们所有的选择性（可以使用类似于 b_f 的公式计算）。将所有桶的选择性贡献相加将得到表达式的整体选择性。图 2 阐明了这个过程。

  • 涉及小于的表达式的选择性可以类似于大于的情况，查看从 0 开始的桶。

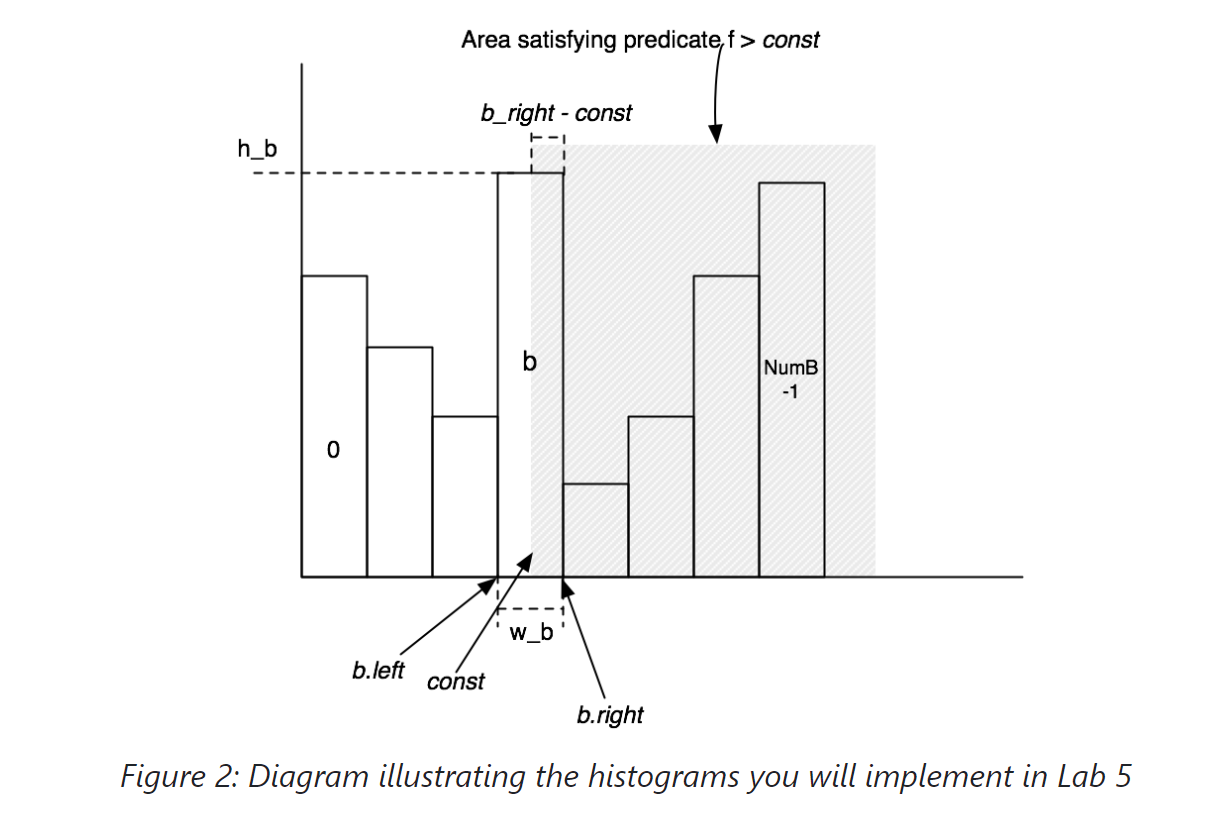
在接下来的两个练习中，您将用代码来执行连接和筛选器的选择性估计。

Exercise 1: IntHistogram.java

你需要实现某种记录表统计信息以进行选择性估算的方法。我们提供了一个骨架类 IntHistogram 用于执行此操作。我们的意图是让你使用上述描述的基于桶的方法来计算直方图，但只要提供合理的选择性估算，你可以自由选择其他方法。

我们提供了一个名为 StringHistogram 的类，它使用 IntHistogram 来计算字符串谓词的选择性。如果你希望实现更好的估算器，你可以修改 StringHistogram，尽管为完成此实验，你可能不需要这样做。

完成此练习后，你应该能够通过 IntHistogramTest 单元测试（如果选择不实现基于直方图的选择性估算，则不必通过此测试）。

Exercise 2: TableStats.java

TableStats类包含一些计算表中元组和页数以及估算谓词在该表字段上的选择性的方法。我们已经创建的查询解析器为每个表创建一个TableStats实例，并将这些结构传递给你的查询优化器（在后续练习中会用到）。

你应该在TableStats中填充以下方法和类：

  1. 实现TableStats构造函数：一旦你实现了跟踪直方图等统计信息的方法，就应该实现TableStats构造函数，添加代码来扫描表（可能多次）以构建你需要的统计信息。
  2. 实现estimateSelectivity(int field, Predicate.Op op, Field constant)：使用你的统计信息（例如，根据字段类型使用IntHistogram或StringHistogram），估算在表上对字段执行谓词操作constant 的选择性。
  3. 实现estimateScanCost()：此方法估算顺序扫描文件的成本，假设读取一页的成本是costPerPageIO。可以假设没有寻找，且没有页面在缓冲池中。该方法可能使用你在构造函数中计算的成本或大小。
  4. 实现estimateTableCardinality(double selectivityFactor)：此方法返回在应用具有选择性selectivityFactor的谓词时关系中的元组数量。该方法可能使用你在构造函数中计算的成本或大小。

你可能需要修改TableStats.java的构造函数，例如，为了进行谓词选择性估算而计算字段上的直方图。

完成这些任务后，你应该能够通过TableStatsTest中的单元测试。

Join Cardinality

最后，注意到上述join计划 p 的成本包括形式为 joincost((t1 join t2) join t3)的表达式。要评估这个表达式，你需要一种估计 t1 join t2的大小（ntups）的方法。这个join基数估算问题比过滤选择性估算问题更为困难。在本实验中，你不需要为此做任何复杂的事情，尽管第2.4节中的一个可选练习包括基于直方图的联接选择性估算方法。

在实现简单解决方案时，你应该记住以下事项：

  • 对于等值连接，当其中一个属性是主键时，连接产生的元组数不能大于非主键属性的基数。
  • 对于等值连接，当没有主键时，很难准确说输出的大小是多少，可能是表的基数的乘积的大小（如果两个表的所有元组都有相同的值）——或者可能是0。可以采用一个简单的启发式方法（例如，两个表中较大表的大小）。
  • 对于范围扫描，关于大小准确说起来同样困难。输出的大小应与输入的大小成比例。可以假设范围扫描发出交叉乘积的固定分数（例如，30%）。通常情况下，范围连接的成本应大于两个大小相同的表的非主键等值连接的成本。

Exercise 3: Join Cost Estimation

JoinOptimizer.java 类包含所有关于连接的排序和计算成本的方法。在这个练习中，你将编写用于估算连接选择性和成本的方法，具体包括：

  • 实现 estimateJoinCost(LogicalJoinNode j, int card1, int card2, double cost1, double cost2)：该方法估算连接 j 的成本，假设左输入的基数为 card1，右输入的基数为 card2，扫描左输入的成本为 cost1，访问右输入的成本为 cost2。你可以假设连接是一个NL连接，并应用前面提到的公式。
  • 实现 estimateJoinCardinality(LogicalJoinNode j, int card1, int card2, boolean t1pkey, boolean t2pkey)：该方法估算连接 j 输出的元组数量，假设左输入的大小为 card1，右输入的大小为 card2，以及指示左和右字段是否唯一（分别是主键）的标志 t1pkey 和 t2pkey。

完成这些方法的实现后，你应该能够通过 JoinOptimizerTest.java 中的单元测试 estimateJoinCostTest 和 estimateJoinCardinality。

Join Ordering

您已经实现了用于评估成本的方法，接下来你将要实现Selinger optimizer。对于这些方法，连接由一系列的join nodes来表达，比如两个表的谓词。而不是像课堂上描述的以连接关系的列表来表示。

将讲义中给出的算法转换成上述的连接节点列表形式，伪代码大纲就是这样：

1
2
3
4
5
6
7
8
9
10
11
1. j = set of join nodes
2. for (i in 1...|j|):
3.     for s in {all length i subsets of j}
4.       bestPlan = {}
5.       for s' in {all length d-1 subsets of s}
6.            subplan = optjoin(s')
7.            plan = best way to join (s-s') to subplan
8.            if (cost(plan) < cost(bestPlan))
9.               bestPlan = plan
10.      optjoin(s) = bestPlan
11. return optjoin(j)

为了帮助您实现这个算法，我们已经提供了几个类和方法来协助你。首先在JoinOptimizer.java中的enumerateSubsets(List v,int size)方法会返回一系列大小为size的v的子集。这个方法十分低效对于大规模的集合。你可以获得额外的学分通过实现更高效的enumertor（提示：考考虑使用in-place生成算法和懒迭代器或流接口来避免将整个幂集具体化）。

此外，我们能提供了如下方法：

1
2
3
4
5
6
private CostCard computeCostAndCardOfSubplan(Map<String, TableStats> stats, 
                                               Map<String, Double> filterSelectivities, 
                                               LogicalJoinNode joinToRemove,  
                                               Set<LogicalJoinNode> joinSet,
                                               double bestCostSoFar,
                                               PlanCache pc)

给定连接的子集（joinSet）和要从该集合中移除的连接（joinToRemove），此方法计算将joinToRemove连接到joinSet - {joinToRemove} 的最佳方式。它以CostCard对象的形式返回这个最佳方法，其中包括成本、基数和最佳连接顺序（作为列表）。如果computeCostAndCardOfSubplan返回null，可能是因为找不到计划（例如，因为没有可能的左深连接），或者所有计划的成本都大于bestCostSoFar参数。该方法使用称为pc（上述伪代码中的optjoin）的先前连接的缓存来快速查找连接joinSet - {joinToRemove}的最快方式。其他参数（stats 和 filterSelectivities）传递到你必须作为练习4的一部分实现的orderJoins方法中，并在下面进行解释。该方法基本上执行先前描述的伪代码的第6到8行。

接下来，我们提供了方法：

1
2
3
4
private void printJoins(List<LogicalJoinNode> js, 
                        PlanCache pc,
                        Map<String, TableStats> stats,
                        Map<String, Double> selectivities)

这个方法可用于显示连接计划的图形表示（例如，当通过优化器的“-explain”选项设置“explain”标志时）。

第四，我们提供了一个名为PlanCache的类，它可以用于缓存到目前为止在你的Selinger实现中考虑的连接子集的最佳连接方式（使用computeCostAndCardOfSubplan需要此类的一个实例）。

Exercise 4: Join Ordering

在JoinOptimizer.java中实现方法：

1
2
3
List<LogicalJoinNode> orderJoins(Map<String, TableStats> stats, 
                   Map<String, Double> filterSelectivities,  
                   boolean explain)

这个方法应该操作 joins 类成员，返回一个新的列表，指定连接应该执行的顺序。列表的第一个项指示左侧最底部的连接在左深计划中的位置。返回的列表中相邻的连接应该共享至少一个字段，以确保计划是左深的。其中，stats 是一个允许你查找查询的 FROM 列表中出现的给定表名的 TableStats 的对象。filterSelectivities允许你查找任何谓词在表上的选择性；它保证对于查询的 FROM 列表中的每个表名都有一个条目。最后，explain 指定你应该输出连接顺序的表示，用于信息目的。

你可能希望使用上述描述的辅助方法和类来帮助实现。大致而言，你的实现应该遵循上述伪代码，循环遍历子集大小、子集和子集的子计划，调用 computeCostAndCardOfSubplan 并构建一个 PlanCache 对象，用于存储执行每个子集连接的最小成本方式。

在实现了这个方法之后，你应该能够通过 JoinOptimizerTest 中的所有单元测试。你还应该通过系统测试 QueryTest。

额外挑战

在本节中，我们将介绍几个可选练习，您可以通过这些练习获得额外学分。这些练习没有前面的练习那么明确，但可以让您有机会展示您对查询优化的掌握！请在报告中明确标出您选择完成的练习，并简要说明您的实施情况和结果（基准数据、经验报告等）。

奖励练习。每项奖励最多可获得 5%的额外学分：

  • 添加代码来执行更先进的连接基数估计。而不是使用简单的启发式搜索来评估连接基数，设计一个更复杂的算法：
    • 一种方法是在每对表 t1 和 t2 中的每对属性 a 和 b 之间使用联合直方图。我们的想法是创建属性a的桶，并为每个 a桶中的桶 A 创建一个与 A 中的 a 值共同出现的 b 值直方图。
    • 估计连接基数的另一种方法是假设较小表中的每个值都与较大表中的一个匹配值相对应。然后，连接选择性的计算公式为：1 /(Max( num-distinct(t1，column1)，num-distinct(t2，column2)))。这里，column1 和 column2 是连接的属性。连接的基数然后是 t1 和 t2 的基数乘以选择性的乘积。
  • 改进子集迭代器。我们的enumerateSubsets实现效率相当低，因为每次调用都会创建大量的Java对象。在这个附加练习中，您将提高enumerateSubsets的性能，以便系统可以在包含20个或更多连接的计划上执行查询优化（目前这样的计划需要几分钟甚至几小时来计算）。
  • 考虑缓存的成本模型。用于估算扫描和连接成本的方法并未考虑缓存在缓冲池中的影响。您应该扩展成本模型以考虑缓存效果。由于多个连接同时运行，这是一个棘手的问题，因此可能难以预测每个连接将使用先前实现的简单缓冲池时将访问多少内存。
  • 改进连接算法和算法选择。我们当前的成本估算和连接操作选择算法（请参见JoinOptimizer.java中的instantiateJoin()）仅考虑嵌套循环连接。扩展这些方法以使用一个或多个附加的连接算法（例如，使用HashMap进行内存哈希）。
  • 丛生计划。改进提供的orderJoins()和其他辅助方法以生成丛生连接。我们的查询计划生成和可视化算法完全能够处理丛生计划；例如，如果orderJoins()返回列表（t1 join t2；t3 join t4；t2 join t3），则对应于一个具有(t2 join t3)节点在顶部的丛生计划。

实现


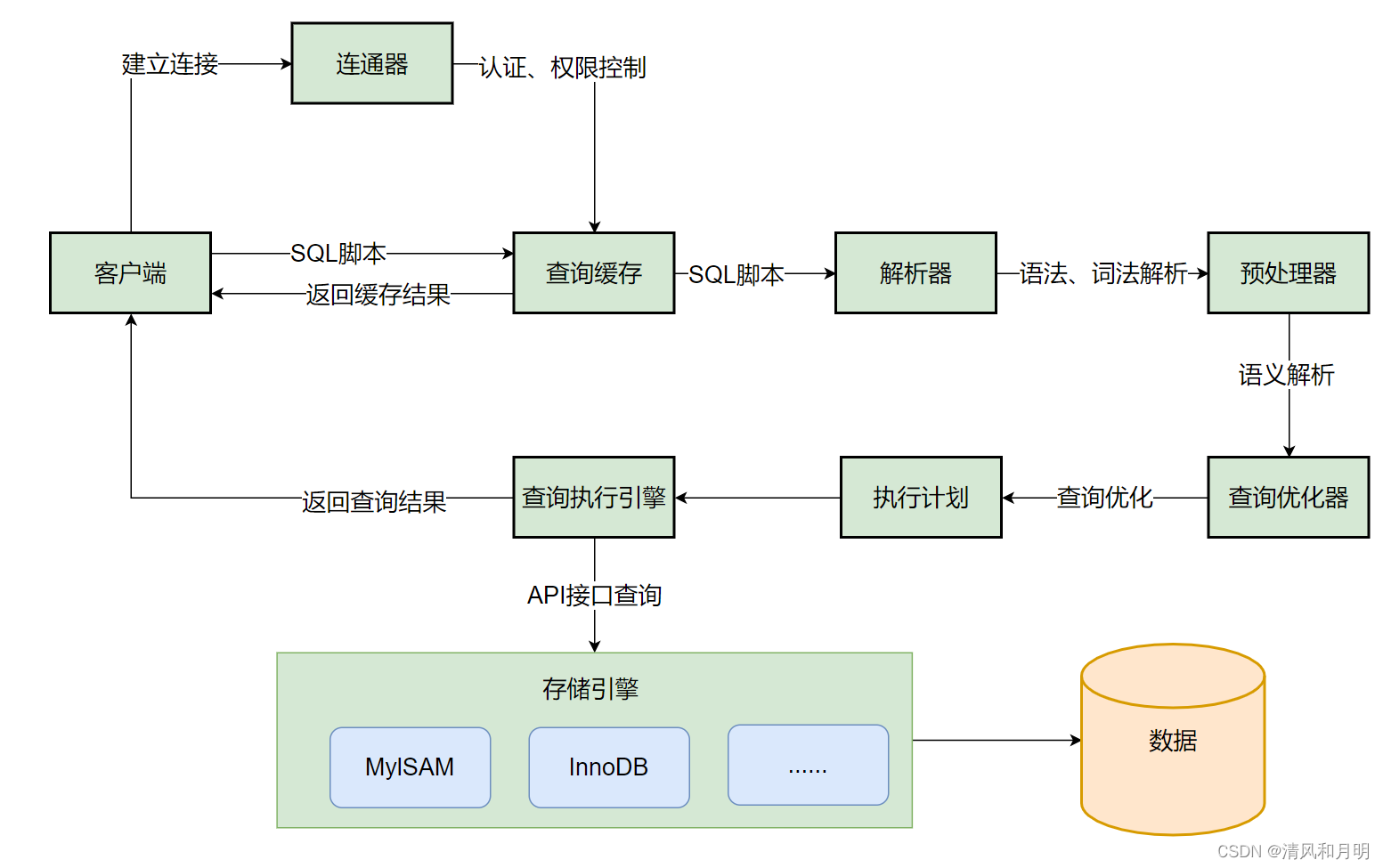
查询优化器：优化器的目的是按照一定原则来得到她认为的目标SQL在当前情形下最有效的执行路径,优化器的目的是为了得到目标SQL的执行计划。

传统关系型数据库里面的优化器分为CBO和RBO两种。
**RBO— Rule_Based Potimizer基于规则的优化器:

RBO所用的判断规则是一组内置的规则，这些规则是硬编码在数据库的编码中的，RBO会根据这些规则去从SQL诸多的路径中来选择一条作为执行计划（比如在RBO里面，有这么一条规则：有索引使用索引。那么所有带有索引的表在任何情况下都会走索引）所以，RBO现在被很多数据库抛弃（oracle默认是CBO，但是仍然保留RBO代码，MySQL只有CBO）

RBO最大问题在于硬编码在数据库里面的一系列固定规则，来决定执行计划。并没有考虑目标SQL中所涉及的对象的实际数量，实际数据的分布情况，这样一旦规则不适用于该SQL，那么很可能选出来的执行计划就不是最优执行计划了。

**CBO—Cost_Based Potimizer基于成本的优化器:

CBO在会从目标诸多的执行路径中选择一个成本最小的执行路径来作为执行计划。这里的成本他实际代表了MySQL根据相关统计信息计算出来目标SQL对应的步骤的IO，CPU等消耗。也就是意味着数据库里的成本实际上就是对于执行目标SQL所需要IO,CPU等资源的一个估计值。而成本值是根据索引，表，行的统计信息计算出来的。(计算过程比较复杂)

本实验是基于CBO的，即评估成本。包括CPU，I/O。Lab3主要针对SQL查询中的查询优化器部分实现。本实验仅需要实现过滤选择性和连接成本。

构建直方图

构建直方图的思想是对于表的每个属性都基于属性的值建立一张直方图，并假设属性的取值尽可能均匀。以此来大致估算在某个谓词下，可能的过滤选择性值为多少。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
public double estimateSelectivity(Predicate.Op op, int v) {  
    switch (op){  
        case EQUALS:{  
            return estimateEqual(v);  
        }  
        case GREATER_THAN:{  
            return estimateGreat(v);  
        }  
        case LESS_THAN:{  
            return 1-(estimateSelectivity(Predicate.Op.GREATER_THAN_OR_EQ,v));  
        }  
        case LESS_THAN_OR_EQ:{  
            return 1-estimateGreat(v);  
        }  
        case GREATER_THAN_OR_EQ:{  
            return estimateGreat(v)+estimateEqual(v);  
        }  
        case LIKE:{  
            return estimateEqual(v);  
        }  
        case NOT_EQUALS:{  
            return 1.0 - estimateEqual(v);  
        }  
    }  
   // some code goes here  
    return -1.0;  
}

public String toString() {  
    StringBuffer sb = new StringBuffer();  
    for (int i = 0; i < this.bctNum; i++) {  
        int w = i== this.bctNum-1?this.max-this.min+1-this.interval*(this.bctNum-1):this.interval;  
        int left = this.min + i*interval;  
        int right = left + w -1;  
        sb.append(String.format("[%d,%d]:%d\n",left,right,this.backets[i]));  
    }  
    return sb.toString();  
}  
  
  
private double estimateGreat(int v){  
    if (v<this.min){  
        return 1.0;  
    }  
    if (v>=this.max){  
        return 0.0;  
    }  
    int idx = vToIdx(v);  
    // to solve difference the width of last backet  
    int w = idx == this.bctNum-1?this.max-this.min+1-this.interval*(this.bctNum-1):this.interval;  
    int h = this.backets[idx];  
    int mod = (v-this.min)-idx*this.interval;  
    double res = 0.0;  
    res += ((w-mod-1)/(w*1.0)) * (h*1.0)/(this.total*1.0);  
    for (int i = idx+1; i < this.bctNum; i++) {  
        res += (this.backets[i]*1.0)/(this.total*1.0);  
    }  
    return res;  
}

上述实现假定某属性取值最大为max,最小为min，桶的数量为bctNum。因此每个桶的区间长度为(max-min+1)/bctNum。如果不能够整除，则最后一个桶的长度会比其他桶多(max-min+1)/%bctNum。比如min=0,max=10,bctNum=3则每个桶负责的区间依次为[0,1,2],[3,4,5],[6,7,8,9,10]。在实现的时候需要特别考虑数落到最后一个桶的情况。

不同的谓词实现技巧：比如大于号和小于等于号的关系。

计算连接成本

连接基数估计
连接基数估计是指在按某些谓词条件下join两个表时，结果中的行数估计值。显而易见，这个值应该不大于M * N，M和N分别指两表的行数。

  • 对于等值连接，即 join on t1.field1=t2.field2。如果field1或field2是主键，那么连接后的指不可能超过非主键表的数量。因为对于非主键表中的每条记录，在主键表中最多只有一条和他匹配。（因为主键不可能重复）。
  • 对于等值连接，且都不是主键的情况。这种情况很难估计，采用了额外挑战中1 /(Max( num-distinct(t1，column1)，num-distinct(t2，column2)))的实现。这里num-distinct指表1中column1去重取值后的集合，也就是有多少个不同的取值。这个评估基于一个前提，认为该属性取每个值的数量是尽可能平衡的。那么对于另一个表中的每条记录，最多有M/num-distinct(t1，column1)*N条记录和它匹配。反之，如果以另一表作为基准，最多有N/num-distinct(t2，column2)*M。取两者的较小值作为评估值即可。（为什么取较小值，因为假设连接的数量为res，res<res1且res<res2即res小于两者较小值。）
  • 对于非等值的连接，同样很难估计。输出的大小应该与输入的大小成正比。假设范围扫描会产生固定比例的交叉积（例如 **30%**）也是可以的。一般来说，范围连接的成本应该大于两个相同大小表的非主键相等连接的成本。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public static int estimateTableJoinCardinality(Predicate.Op joinOp,  
                                               String table1Alias, 
                                               String table2Alias,String field1PureName,  
                                               String field2PureName, 
                                               int card1, int card2,
                                               boolean t1pkey,boolean t2pkey, 
                                               Map<String, TableStats> stats,  
                                               Map<String, Integer> tableAliasToId) {  
    int card = 1;  
    // some code goes here  
    if (joinOp.equals(Predicate.Op.EQUALS)){  
        if (t1pkey || t2pkey){  
            if (t1pkey && !t2pkey){  
                card = card2;  
            }else if (!t1pkey && t2pkey){  
                card = card1;  
            }else{  
                card = Math.min(card1,card2);  
            }  
        }else{  
            // improved method  
            Integer tabldId1 = tableAliasToId.get(table1Alias);  
            Integer tabldId2 = tableAliasToId.get(table2Alias);  
            String tableName1 = Database.getCatalog().getTableName(tabldId1);  
            String tableName2 = Database.getCatalog().getTableName(tabldId2);  
            TableStats stats1 = stats.get(tableName1);  
            TableStats stats2 = stats.get(tableName2);  
            int distinct1 = stats1.getFieldDistinct(Database.getCatalog().getTupleDesc(tabldId1).fieldNameToIndex(field1PureName));  
            int distinct2 = stats2.getFieldDistinct(Database.getCatalog().getTupleDesc(tabldId2).fieldNameToIndex(field2PureName));  
            return (int)((card1 * card2 * 1.0)/(Math.max(distinct1,distinct2)));  
        }  
    }else{  
        return Math.max((int)(0.3*(card1 * card2)),Math.max(card1,card2));  
    }  
    return card <= 0 ? 1 : card;  
}

计算连接顺序

考虑到不同的连接顺序产生的成本不同。
比如t1 join t2的成本大致为：
card1 * card2 * 1.0 + cost1 + card1 * cost2
而t2 join t1的成本大致为：
card1 * card2 * 1.0 + cost2 + card2 * cost1
我们需要计算给定的查询计划中，可能的连接顺序成本最小的方案。这里通过DFS枚举了所有连接顺序，然后通过DP算法来计算每种连接次序所需的成本。假设对于需要join的三个节点A,B,C,我们如果知道了A,B连接（可能的其中一个子计划）具有最小成本的顺序为AB,那么只需要考虑C(AB),(AB)C，当然还需要考虑将BC或AC先连接的情况。我们称AB,BC,AC为子计划，将他们进行缓存，之后就可以快速得到A和B，B和C，A和C连接的最佳顺序。源文件提供了给定连接的子集（joinSet）和要从该集合中移除的连接（joinToRemove），此方法计算将joinToRemove连接到joinSet - {joinToRemove} 的最佳方式。上述的C
节点在这是joinToRemove，s是指集合{A,B,C}。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public List<LogicalJoinNode> orderJoins(  
        Map<String, TableStats> stats,  
        Map<String, Double> filterSelectivities, boolean explain)  
        throws ParsingException {  
  
    // some code goes here  
    //Replace the following    PlanCache pc = new PlanCache();  
    CostCard bCard = null;  
    for (int i = 1; i <= this.joins.size(); i++) {  
        Set<Set<LogicalJoinNode>> jsSets = enumerateSubsets(this.joins, i);  
        for (Set<LogicalJoinNode> s : jsSets) {  
            CostCard bestCard = null;  
            for (LogicalJoinNode remove : s) {  
                CostCard costCard = computeCostAndCardOfSubplan(stats, filterSelectivities, remove, s, bestCard==null?Double.MAX_VALUE:bestCard.cost, pc);  
                if (costCard!=null){  
                    if (bestCard==null || (bestCard!=null&&costCard.cost<bestCard.cost)){  
                        bestCard = costCard;  
                        if (i==this.joins.size()){  
                            bCard = costCard;  
                        }  
                    }  
                }  
            }  
            if (bestCard!=null){  
                pc.addPlan(s,bestCard.cost,bestCard.card,bestCard.plan);  
            }  
        }  
    }  
    List<LogicalJoinNode> js = this.joins;  
    if (bCard!=null){  
        js = bCard.plan;  
    }  
    if (explain){  
        printJoins(js,pc,stats,filterSelectivities);  
    }  
    return js;  
}