第二章

Gauss消去法


列主元法

Doolittle三角分解

适用条件：顺序主子式都不能为0



Cholesky分解

适用条件：适用于对称正定矩阵

矩阵的条件数








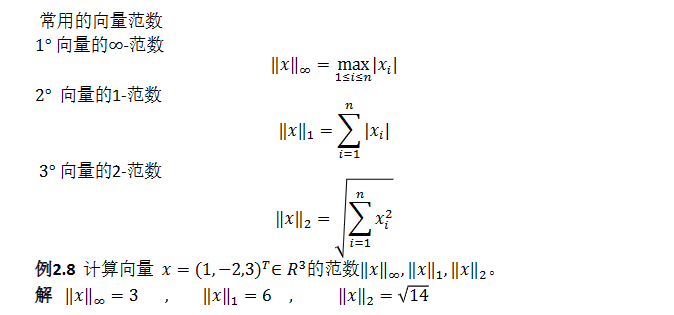
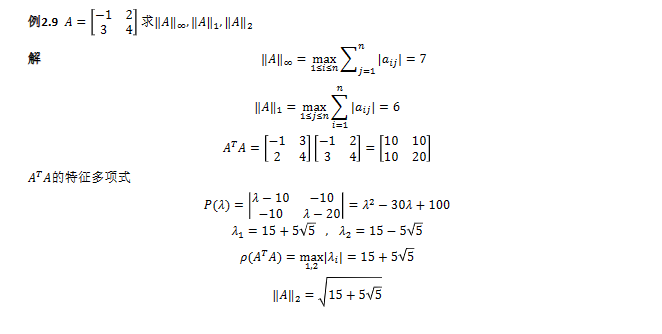
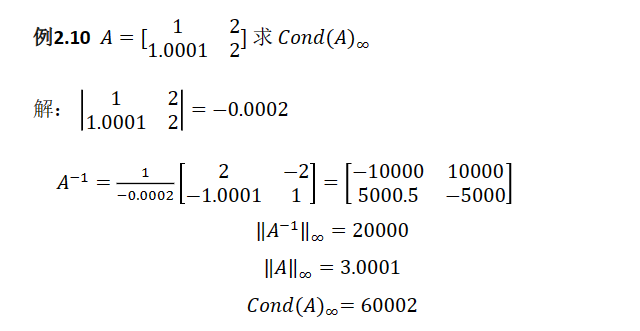
课后习题


第三章


Jacobi迭代法

Gauss-Seidel迭代法

迭代收敛性（重要）



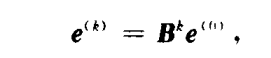
因为$ρ(B)\leq||B||$，所以判断$||B||_1或||B||_2或||B||_\infty是否\lt1$即可



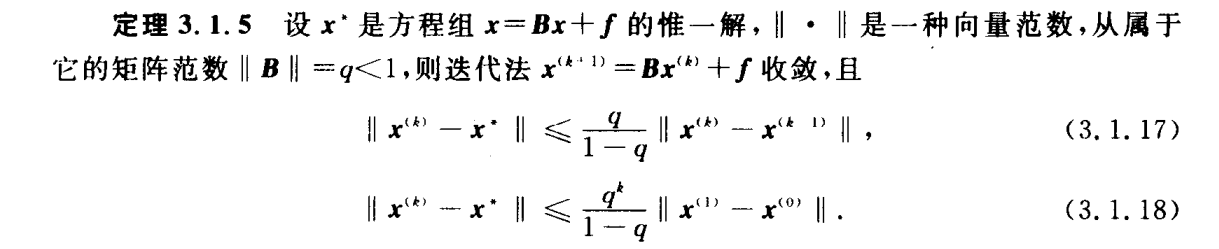
SOR迭代法



课后习题

第四章

二分法和试位法

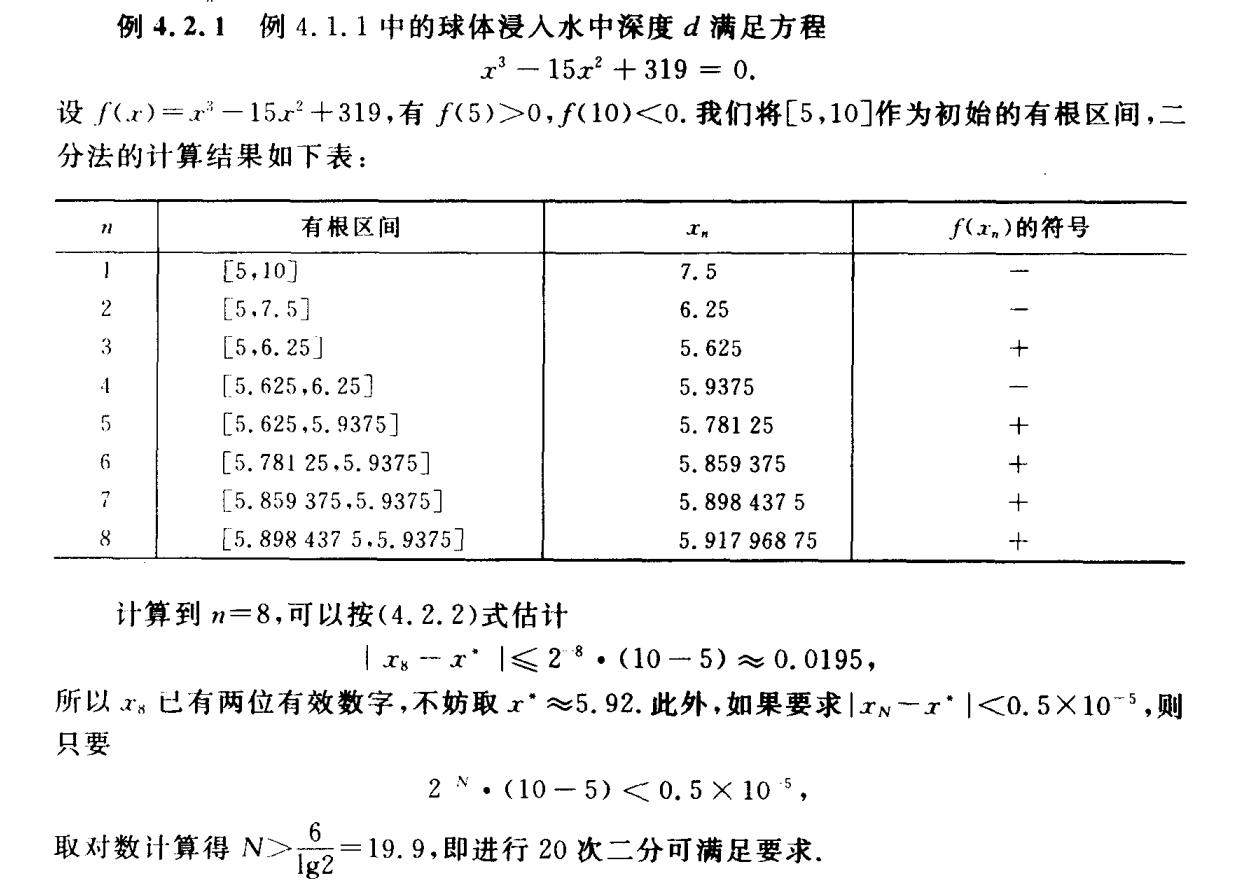
迭代法





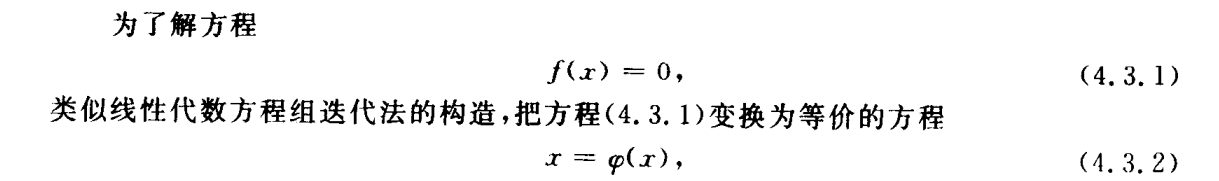
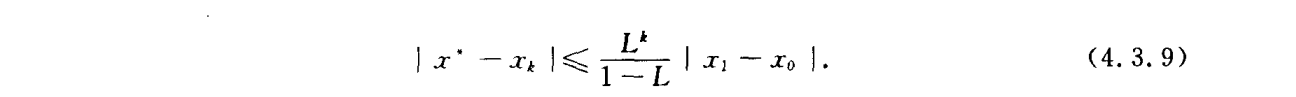
局部收敛性



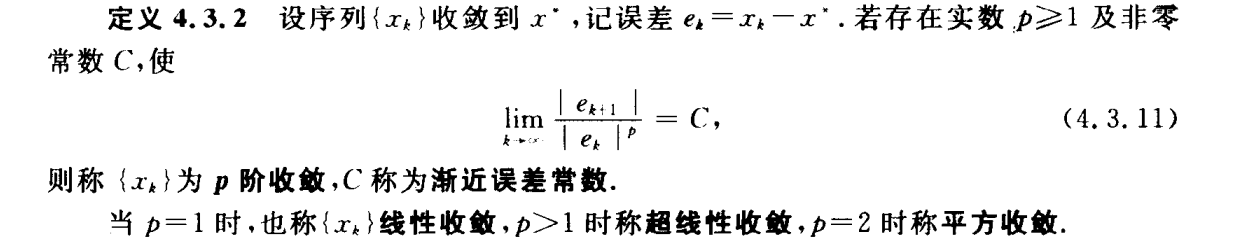
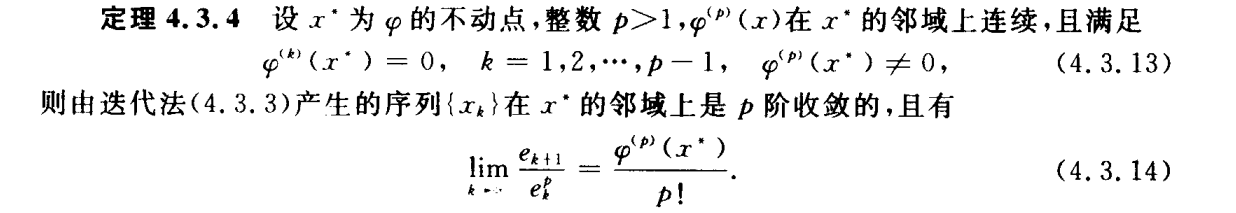
上述公式是判断迭代法几阶收敛的关键。如果一阶导数不为0，那么是线性收敛的。

迭代加速Aitken和Steffensen

Newton迭代法



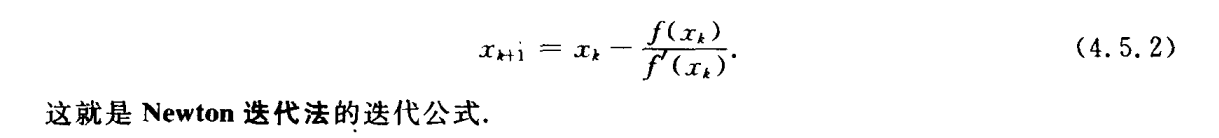
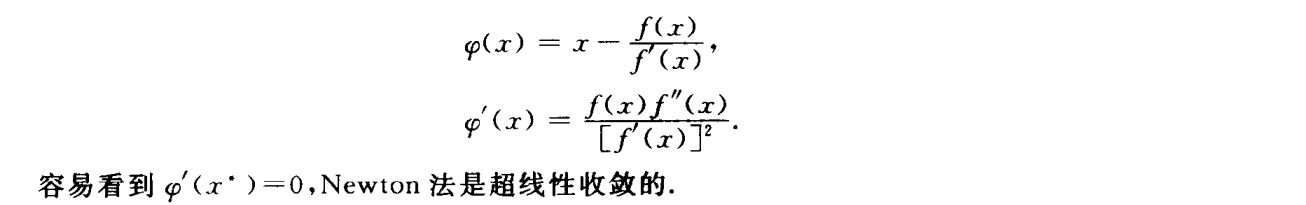
重根
方法一：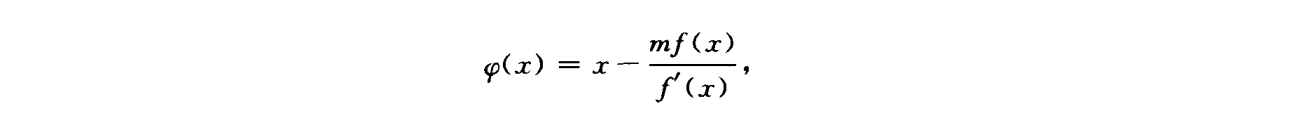

方法二：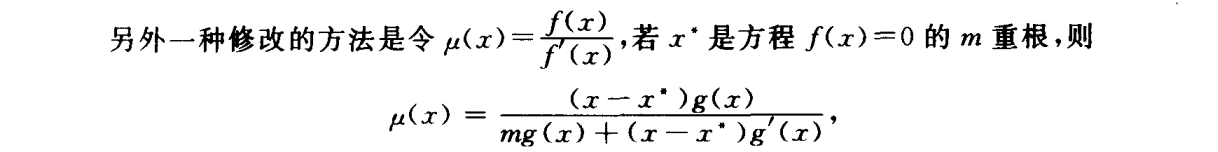

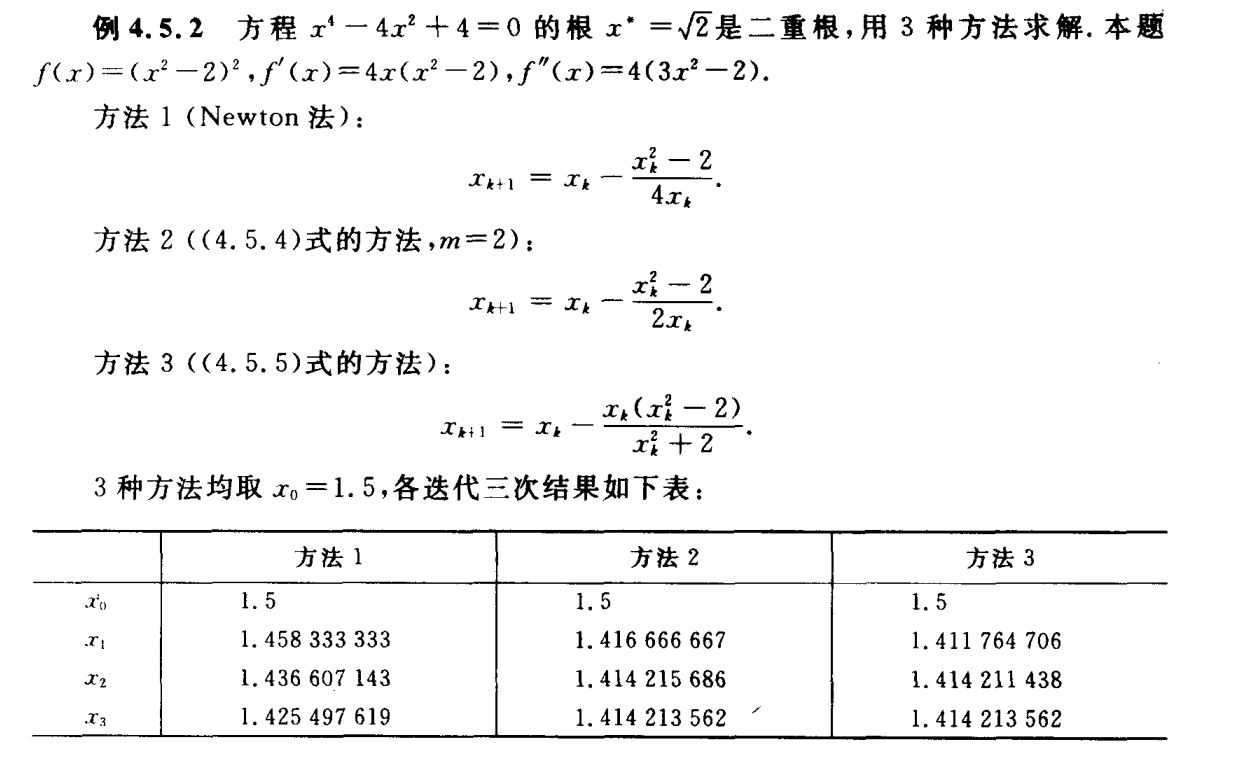
非线性方程组不动点迭代

非线性方程组Newton法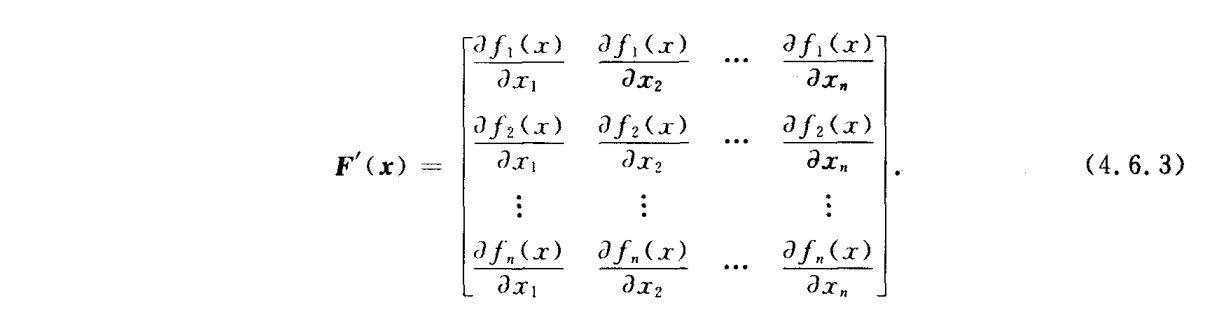


第六章

Lagrange





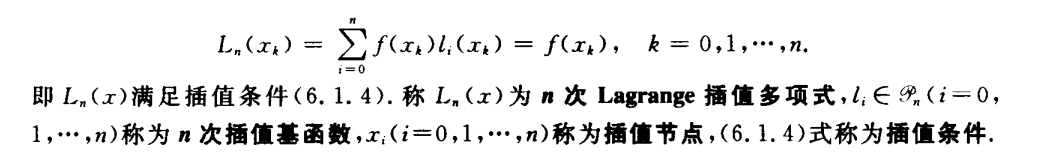
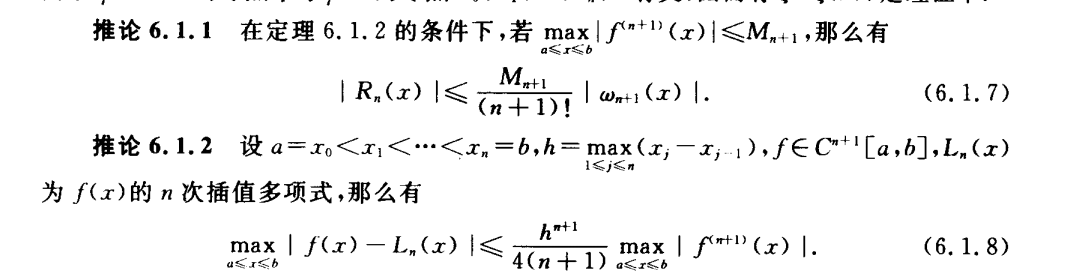
均差和重节点均差


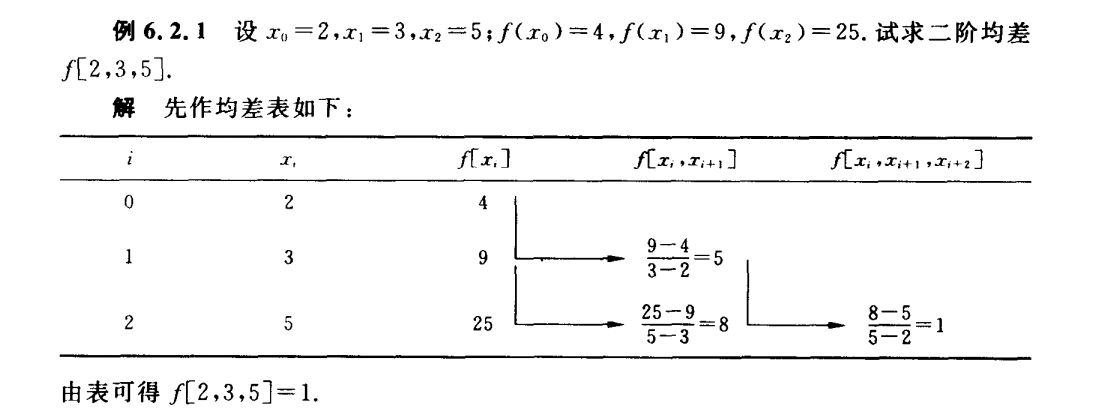
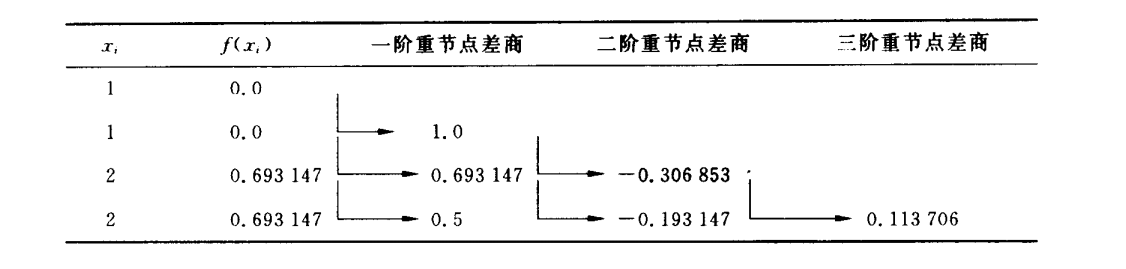
Newton插值法



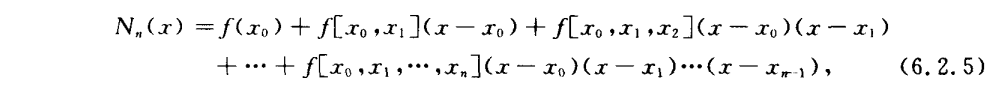
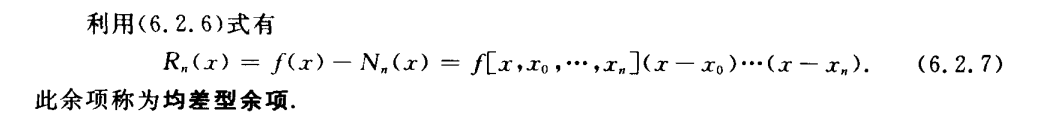
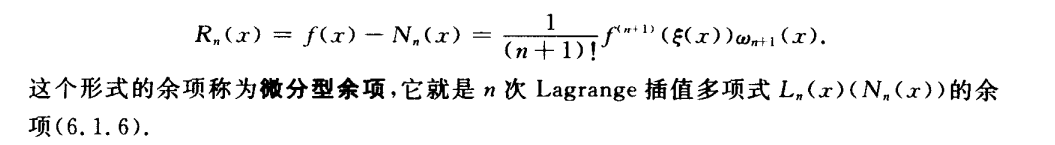
Newton-Hermite插值


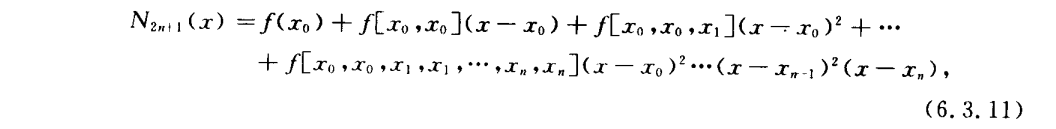
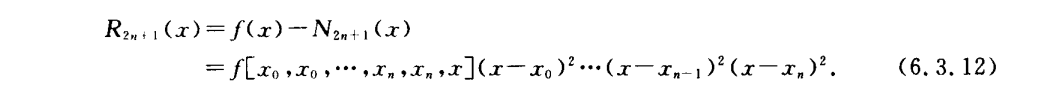
分段线性插值


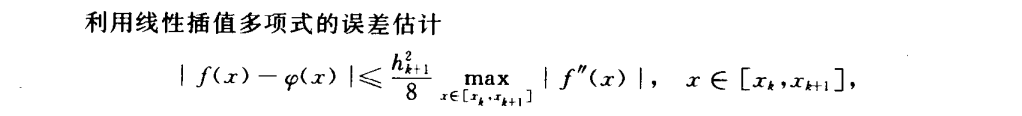
分段三次Hermite插值

三次样条插值

不仅一阶导，二阶导也连续

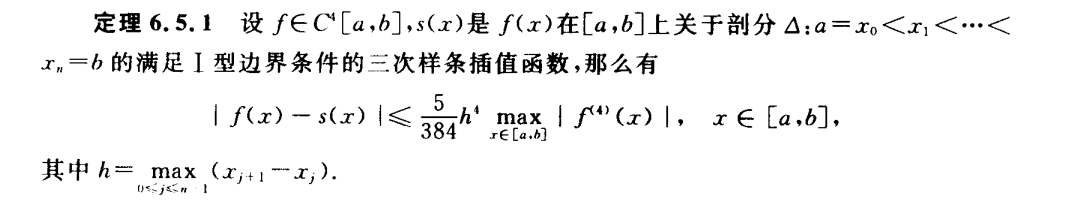
第七章

正交多项式



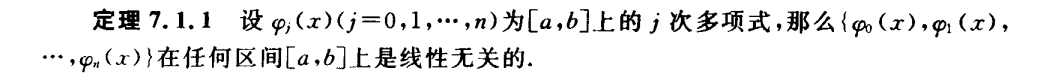
最小二乘法

第八章

梯形和Simpson

用一次和二次Lagrange插值近似积分函数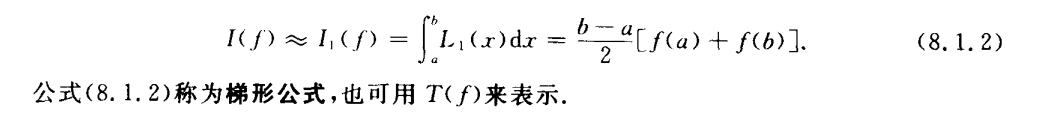


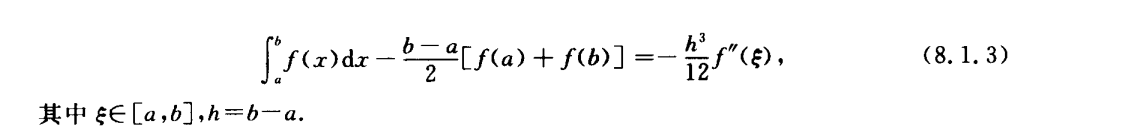
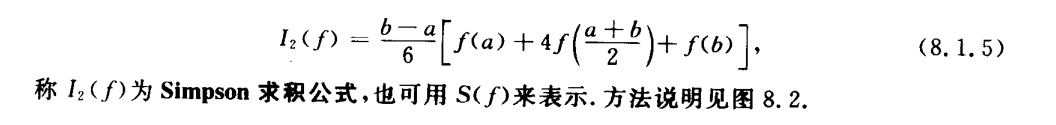
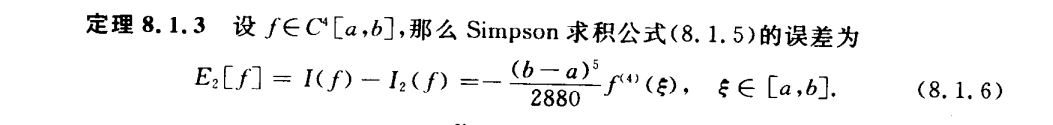
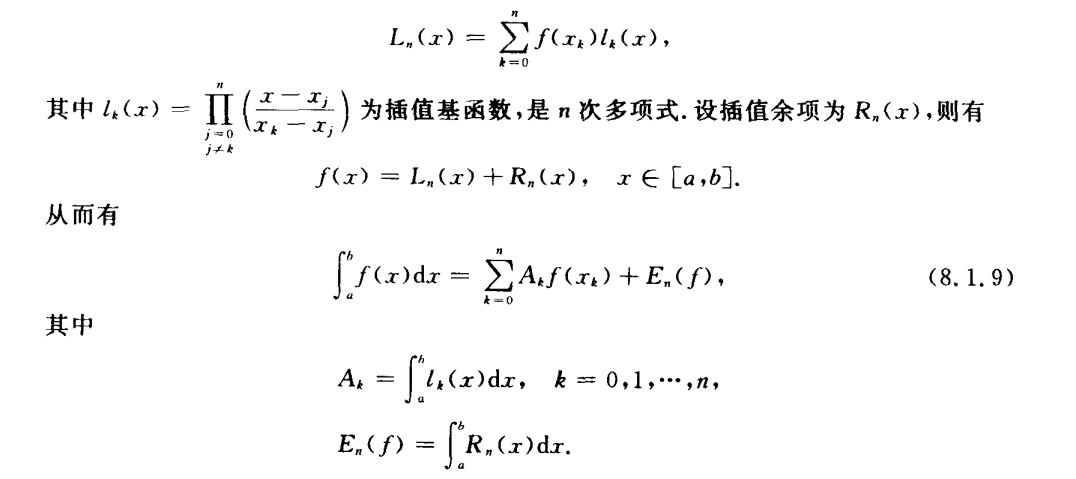
代数精度

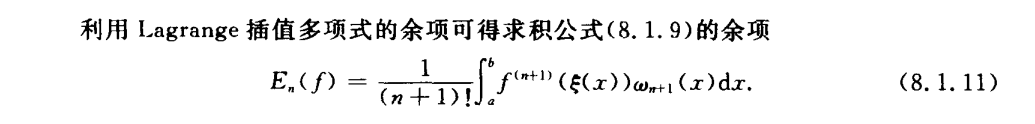
Gauss求积和构造


记住一个特殊的权函数和节点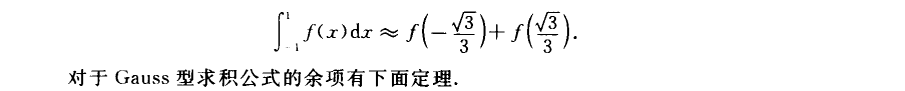

不在[-1,1]上的可以通过转换映射（去年题5）

Gauss-Legendre求积




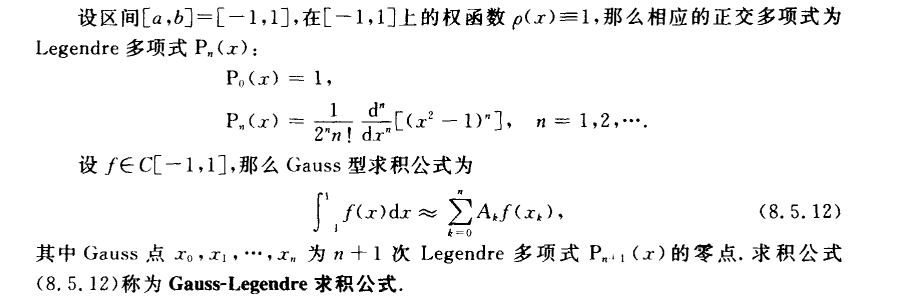
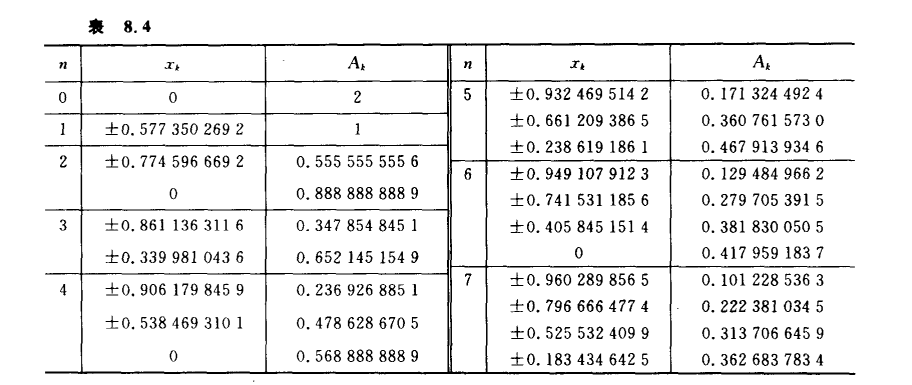
Gauss-Chebyshev求积



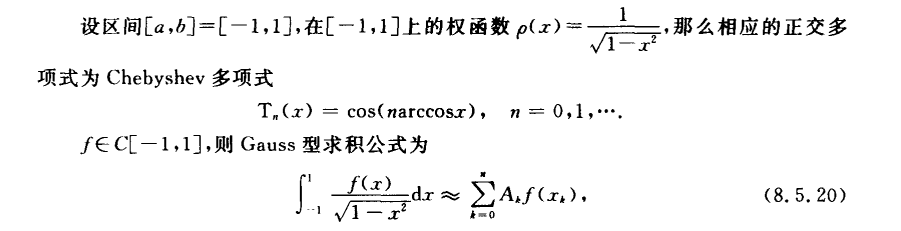
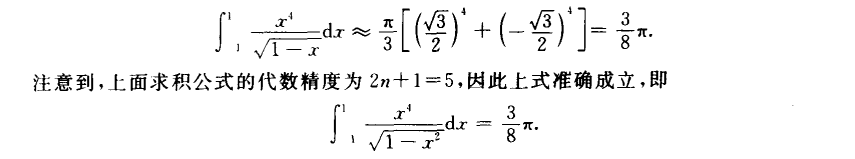
第九章

显式Euler

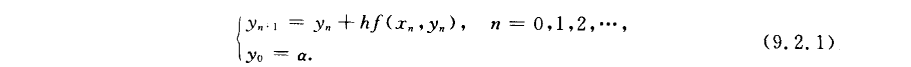
隐式Euler

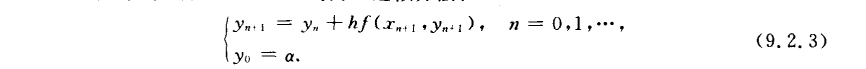
梯形

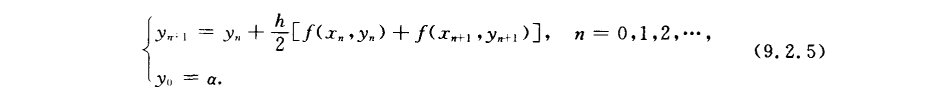
改进Euler

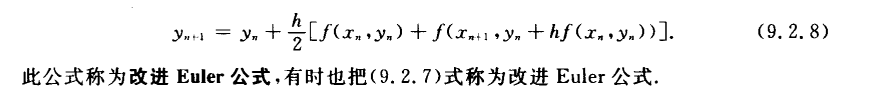
泰勒公式

误差



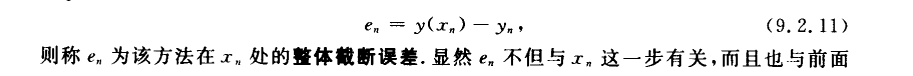
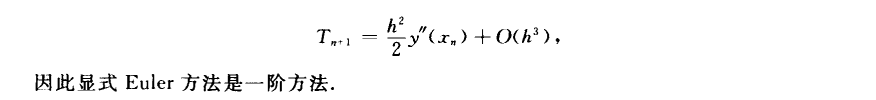
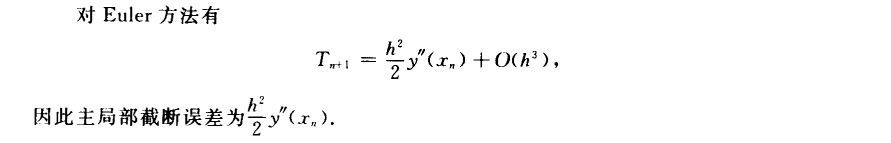
Runge-Kutta方法

记几个重要的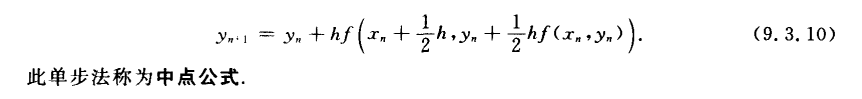


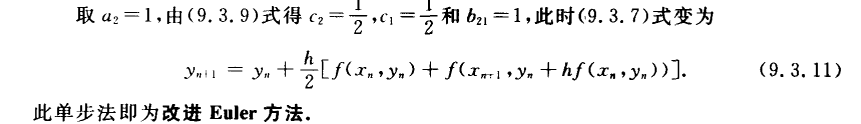
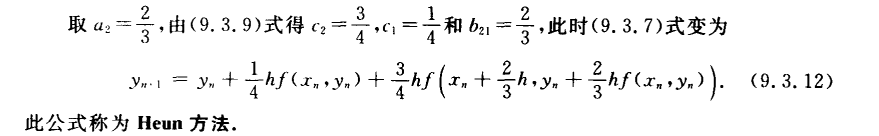
相容性、收敛性、绝对稳定性

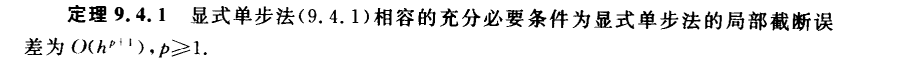
考点

第一章

  • 误差
  • 有效数字
  • 数值方法的稳定性

第二章

  • Gauss消去法，列主元
  • A=LU分解
  • Cholesky分解
  • 矩阵范数计算
  • 条件数计算
  • 误差分析

第三章

  • 迭代法
  • 收敛条件和收敛速度
  • Jacobi和Gauss-Seide迭代法
  • 分量形式、迭代矩阵、收敛的充要条件、充分条件
  • SOR迭代，求解最佳松弛因子
  • 最速下降，共轭梯度不考

第四章

  • 不动点迭代
  • 局部收敛性、收敛阶计算
  • 加速方法
  • Newton迭代，收敛性，单根、重根收敛阶
  • 非线性方程组不考

第五章（不是重点，很可能不考）

  • Householder
  • Givens
  • 幂法、反幂法
  • QR算法（不考）
  • 带位移算法

第六章（感觉出大题）

  • Lagrange、Newton、Hermite
  • 插值方法，余项
  • 均差，重节点均差计算（填空）
  • 分段低次插值以及三次样条插值函数计算（大题）

第七章

  • 正交多项式
  • 最小二乘法（填空）
  • 线性以及特殊非线性化成线性问题（大题）

第八章（感觉出大题）

  • 梯形公式，Simpson
  • 代数精度
  • Romberg积分
  • Gauss型相关

第九章（感觉出大题）

  • 单步法：Euler、隐式Euler、梯形、改进Euler
  • Runge-Kutta方法
  • 局部截断误差，主项，方法阶，相容性，收敛性，绝对稳定性
  • 线性多步法