工程硕士数学
1.引论
正交矩阵
2.线性代数方程组的直接解法
2.2Gauss消去法
2.3三角分解
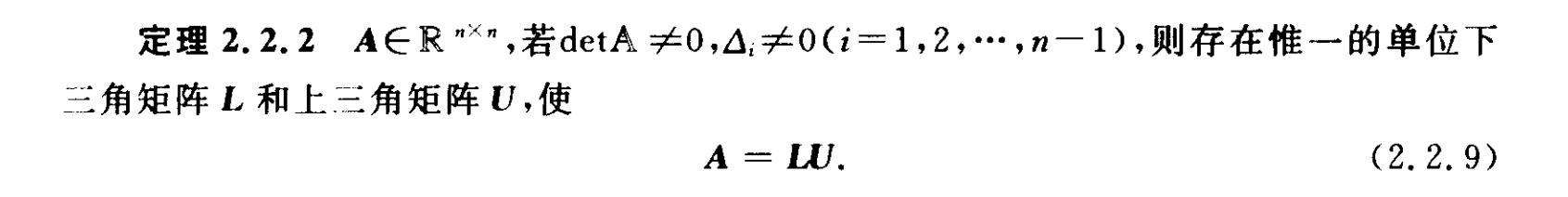
2.3.1直接三角分解
适用于所有情况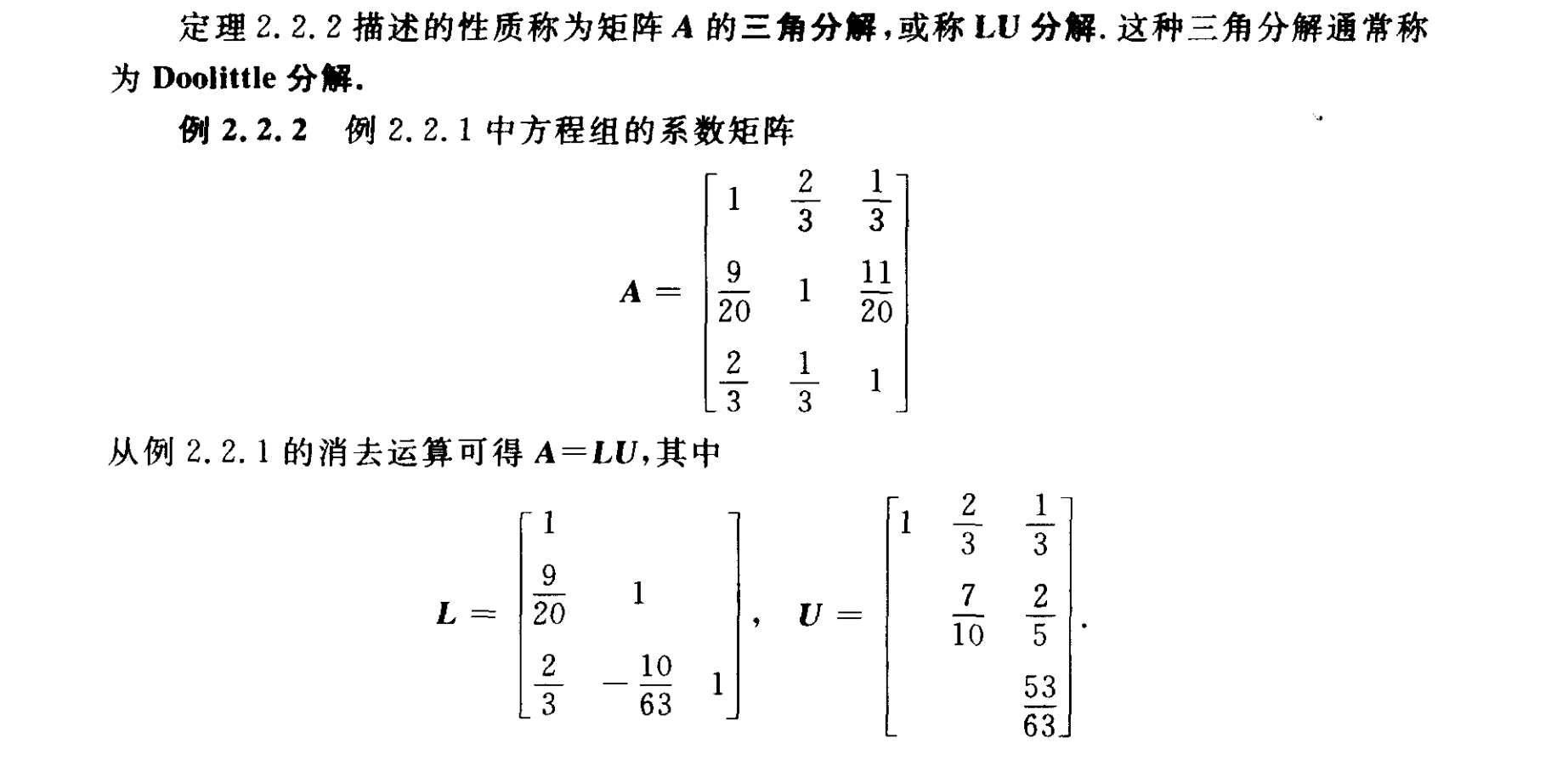
规律:下三角阵L第一列和A第一列一致,上三角阵U第一行和A第一行一致
2.3.2追赶法
只适用于三对角矩阵
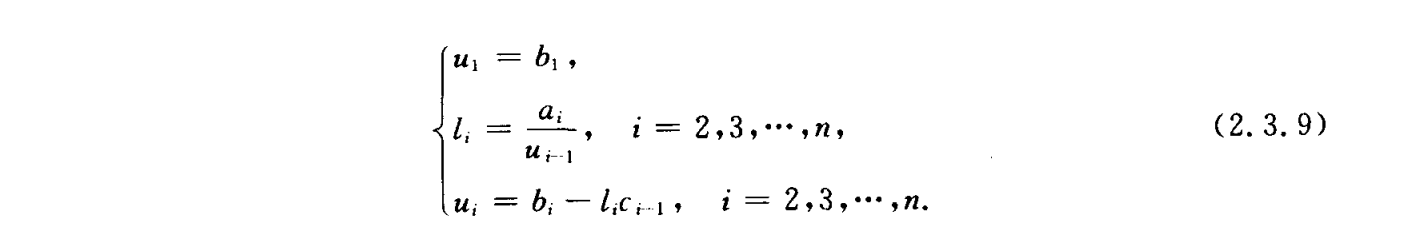
2.4列主元消去法
是对Gauss消去法的优化,每次从待消元的所有行中的指定列中选出绝对值最大的作为主元


2.5对称正定矩阵
2.5.1对称正定矩阵的三角分解

更特别的(平方根法)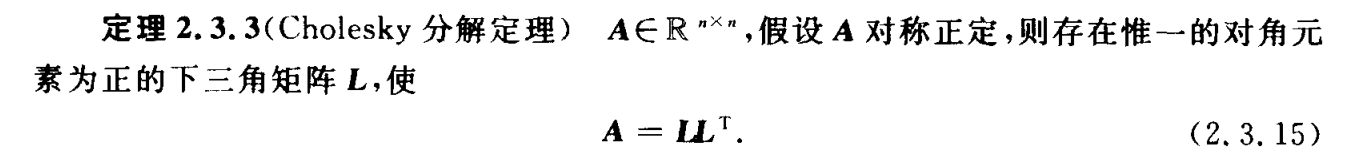
证明: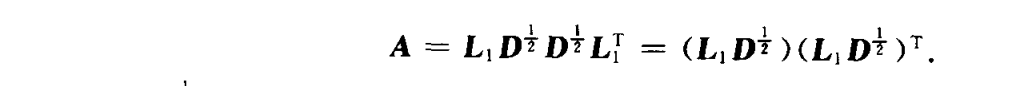
向量范数

常用向量范数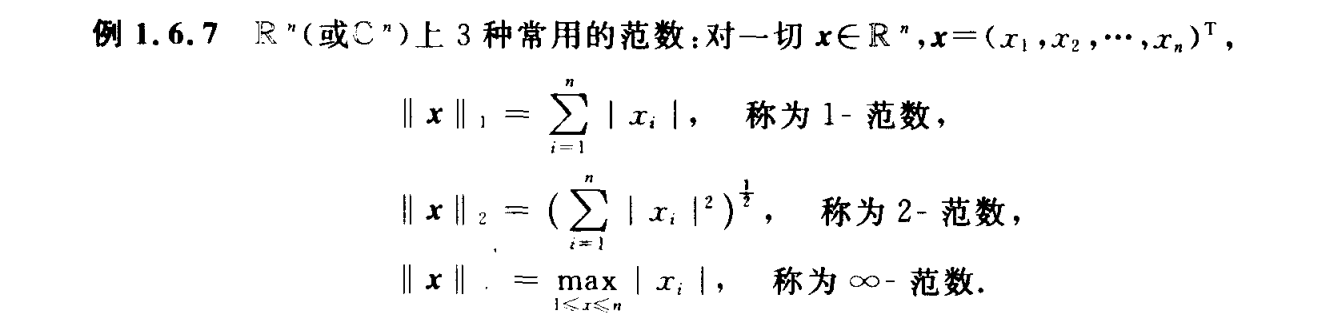
矩阵范数
算子范数
可以看成矩阵A作用在全部向量上产生的效果的比例最大的那个值,即为||A||

谱半径是其对应矩阵的特征值中最大的特征值绝对值

条件数与所选择的范数有关,不同范数计算的条件数不同


如何证明:
1)A的某一行和该行对应的代数余子式相乘在相加后结果为该行列式的值
2)A的某一行和另一行元素的代数余子式相乘在相加后结果为0(相当于两行相同的行列式展开)
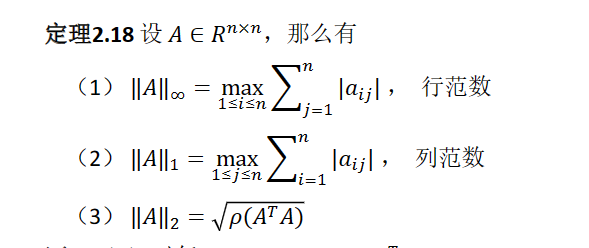
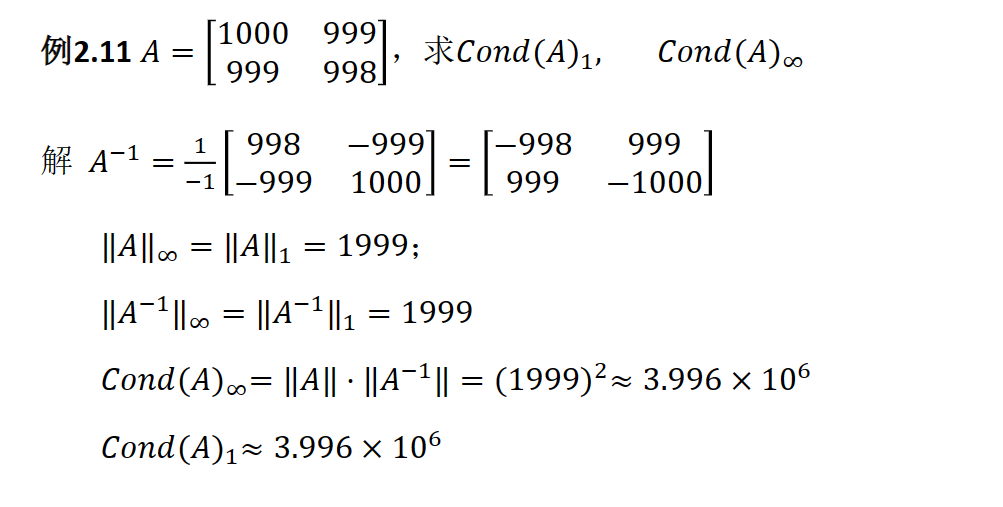
线性方程组-迭代法 0.1:范数与谱半径 - 知乎 (zhihu.com)
$(1)Cond(A)≥1$
$(2)若A是正交矩阵 A^TA=I,那么Cond(A)_2=1$
$(3)设U为正交矩阵,Cond(A)_2=Cond(AU)_2=Cond(UA)_2$
$(4)设\lambda_1和\lambda_n分别为A的模的最大和最小特征值,那么Cond(A)≥\frac {\vert\lambda_1\vert}{\vert\lambda_n\vert} 特别地,A对称则Cond(A)_2=\frac {\vert\lambda_1\vert}{\vert\lambda_n\vert}$

方程组的解对A或b的扰动可能是敏感的,称方程组是病态方程组,病态与否取决于*A
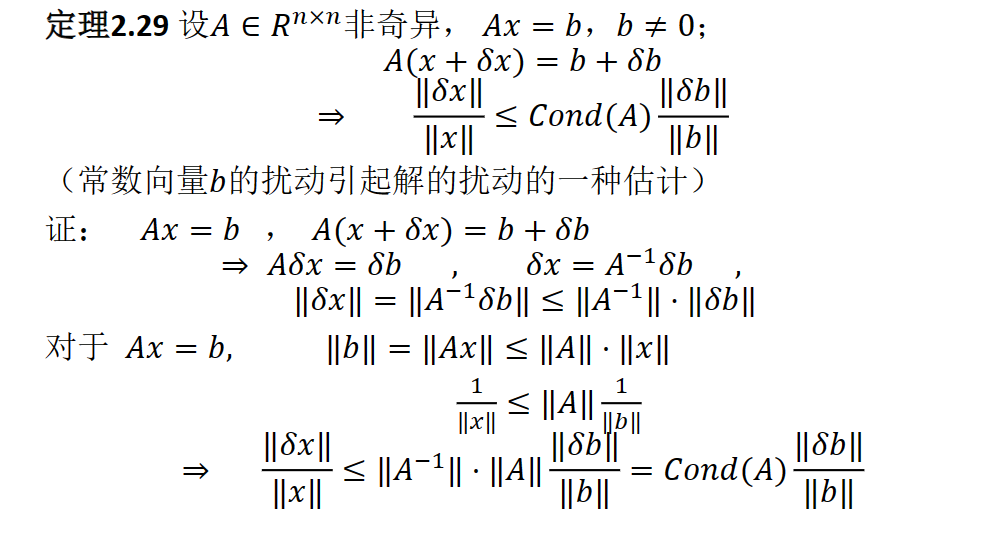
作业
第一次作业
P37:13(2),19
P62-64:2,3,6,10,11
P62-64
(2)
1 | 2.680000 3.040000 -1.480000 | -0.530000 |
3.线性代数方程组的迭代法

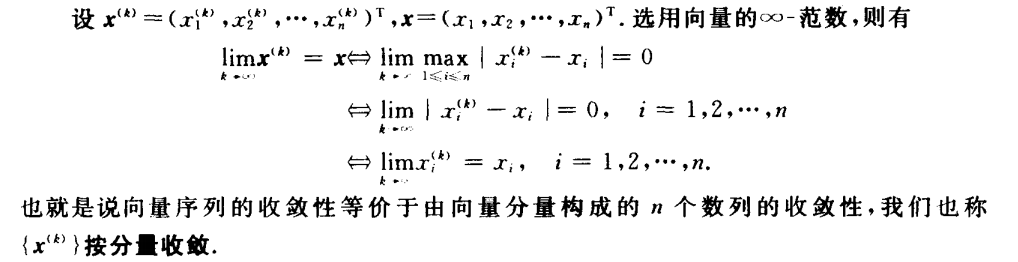

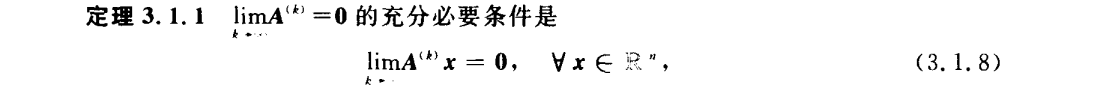
Jacobi迭代法

Gauss-Seidel迭代法
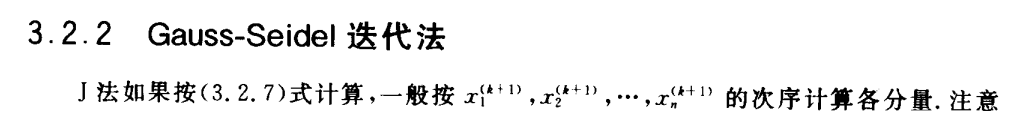

收敛性分析




SOR迭代法

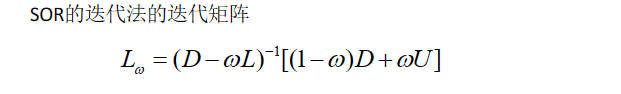
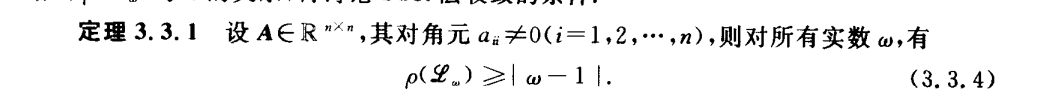
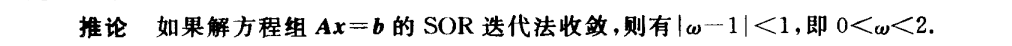
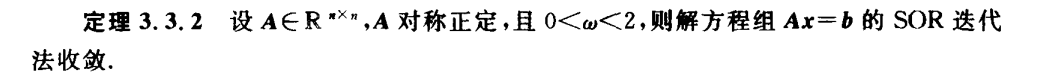

最速下降法
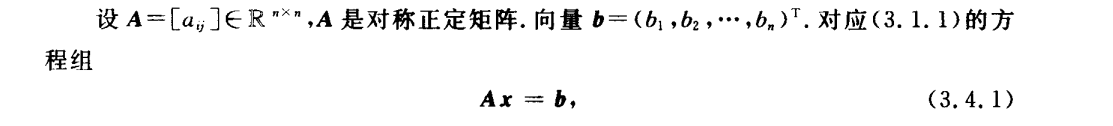



共轭梯度法

4.非线性方程和方程组的数值解法

想象一个抛物线 $y=(x-1)^2$,$x=1$是二重根
二分法


C[a,b]表示[a,b]上的连续函数
$C^k$[a,b]表示的是k阶可导且导函数连续

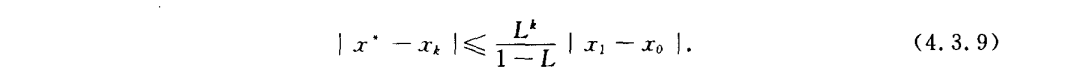

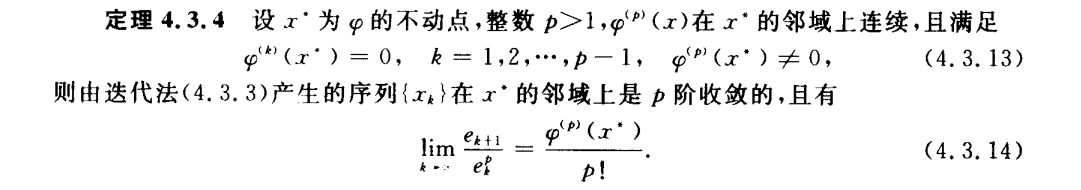

5.矩阵特征值的计算方法


5.2正交变换和矩阵分解

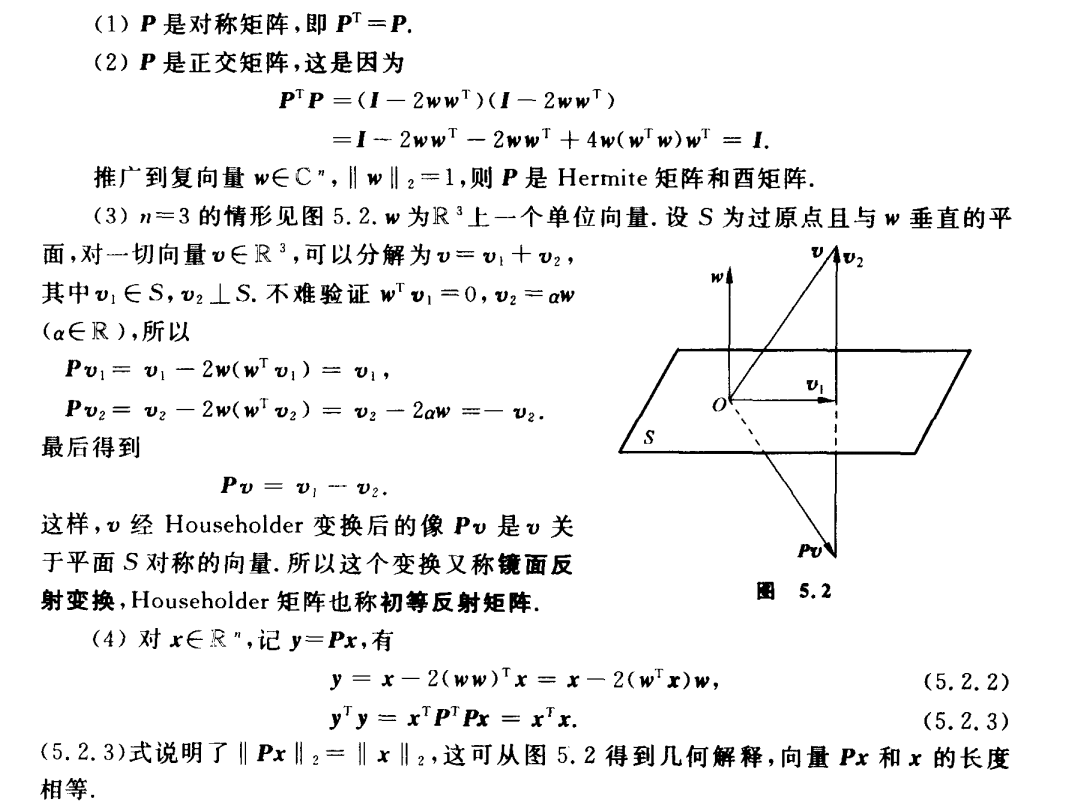


给出了一种方法可以使得范数相同的向量变换为部分连续分量为0的向量
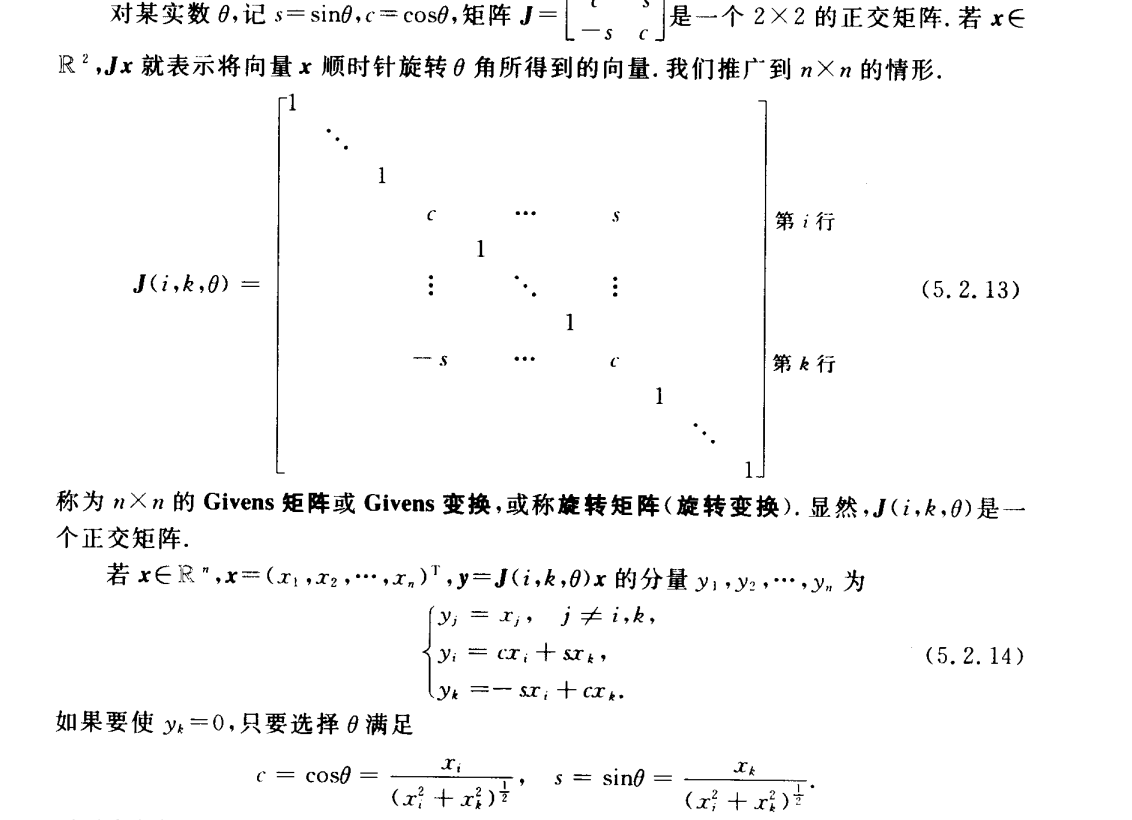

给出了一种方法可以使得范数相同的向量变换为第k个分量为0的向量

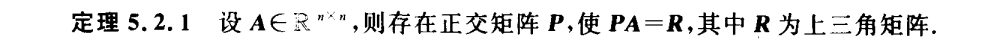





6.插值法