1.作业简介

Treemap（树状图）是一种数据可视化技术，通常用于展示层次结构数据的比例关系。它将数据以嵌套矩形的形式呈现，其中每个矩形代表一个数据单元，而矩形的大小表示数据单元的相对大小，通常是基于某种特定属性或值的比例。Treemap 是一种有效的方式，可以帮助可视化复杂的层次数据，并理解数据之间的层次关系以及数据的相对重要性。

然而创建具有清晰结构和信息丰富的Treemaps可能是一项具有挑战性的任务，需要仔细考虑数据、布局、可视化美学和用户交互等多个方面。例如，矩形布局化算法是Treemap中最为核心的一步。通过合理安排矩形的布局，尽可能使得矩形的长宽相近，从而避免“细长条”矩形的出现，“细长条”矩形不利于呈现矩形间的权重关系，因此需要设计巧妙的算法，让矩形的横纵比减少。本实验基于论文[1]中给出的Squarified treemaps算法，并进行优化，实现了树状图的可视化。

本实验共实现了以下三种不同的Treemaps：

  • Squarified treemaps：根据论文中给出的算法进行了实现
  • Squarified treemaps++：优化了矩形排列算法，从而降低了整体矩形的横纵比
  • Nested Tree-Map：通过递归，从而实现了父-子层次关系的呈现效果

2.Squarified treemaps实现

2.0 数据结构说明

由于最终需要将矩形进行可视化，绘制在画布上，定义矩形结构如下：

  • x：矩形左下角的横坐标，即x坐标
  • y：矩形左下角的纵坐标，即y坐标
  • dx：矩形的横向距离，也可理解为“宽”
  • dy：矩形的纵向距离，也可理解为“高”
  • v：矩形的面积或权重

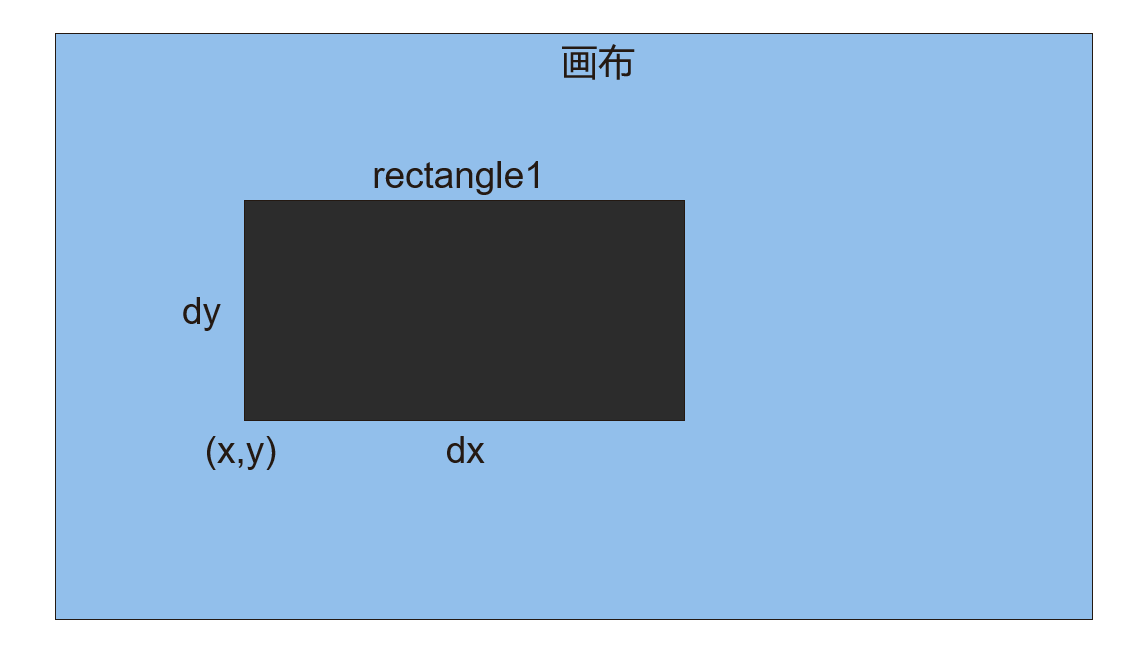
    因此，通过(x,y)以及dx和dy可以唯一确定一个矩形的位置和其形状。因此通过矩形布局化算法确定每个矩形的位置和形状后，再使用Matplotlib进行绘制。

另外，为方便起见，定义画布的左下角为原点，即x=0，y=0，这与数学中的二维坐标轴是相似的。

2.1实现原理

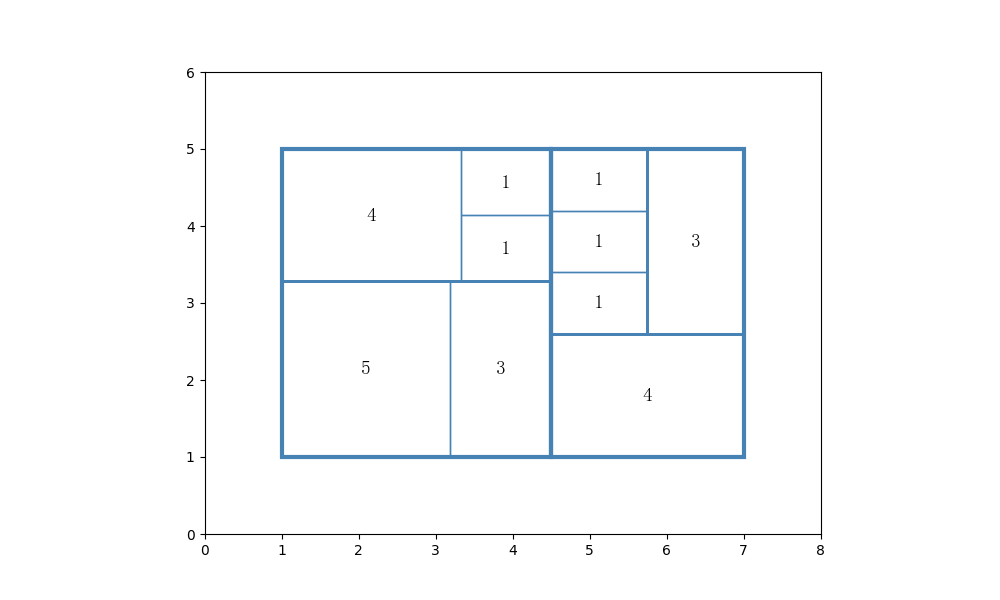
本算法需要实现将一组非负数值如$[6,6, 4,3,2,2,1]$作为输入，并将这些数值作为权重（在本算法中以矩形的面积表示）在一个长和宽确定的大矩形中细分为面积依次为6，6，4，3，2，2，1的七个子矩形，且要求矩形的横纵比尽可能小，也就是尽可能避免“细矩形”的出现。

算法整体基于贪心法，即意味着在较低时间复杂度的情况下，尽可能取得较好的效果，但在大部分情况下达不到最优解。算法思路如下：

  • 将矩形按照权重降序排列，因为在通常情况下，先划分较大的矩形往往能达到更好的效果。
  • 每次从待划分的矩阵队列中取出第一个矩阵，进行划分。划分基于如下两种决策，决策结果由能否改善当前行最差的横纵比决定。
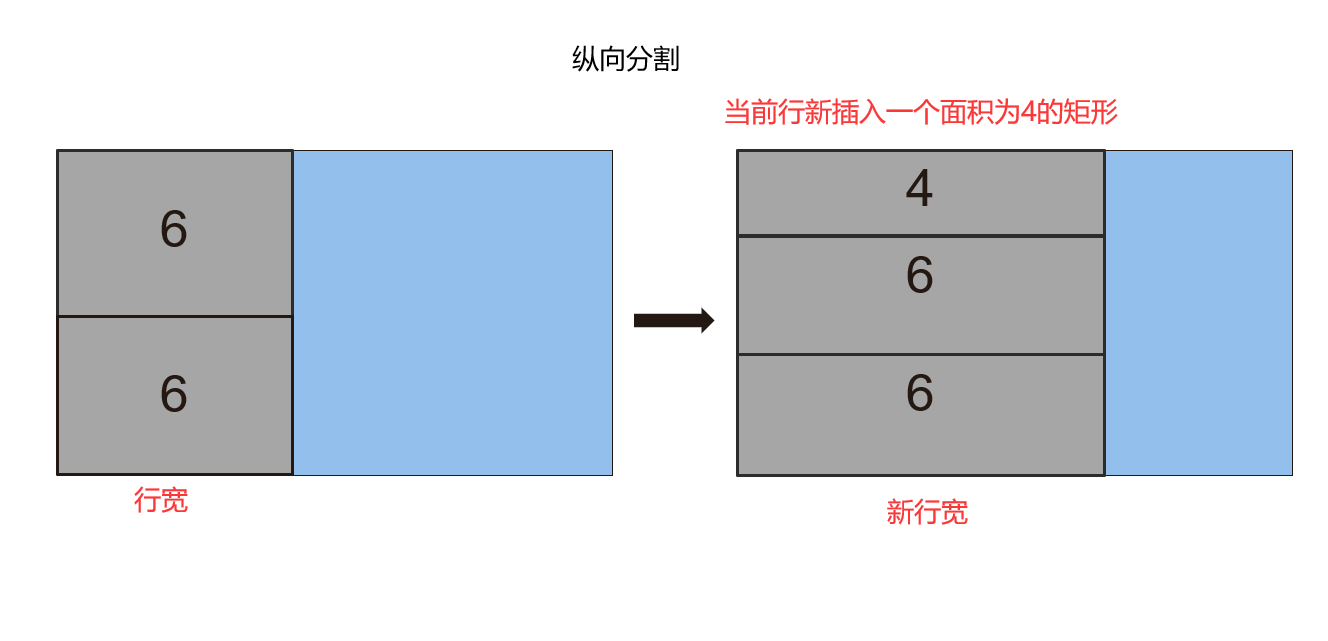
    • 将矩形添加到当前行，则意味着需要调整当前行之前已经被放置的矩形的宽度。
    • 固定当前行，在剩下的子矩形中，开始新行，并将当前矩形添加进去。
  • 直至所有矩形被排列完毕，进行绘制可视化结果。

函数原型

treemap函数：是整个算法的main函数，可理解为入口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def treemap(x,y,dx,dy,rec_lst:[float]):  
    '''  
    主函数  
    :param x: 从(x,y)点开始排列  
    :param y: 从(x,y)点开始排列  
    :param dx: 总横向距离（或理解为画布的横向距离）  
    :param dy: 总纵向距离（或理解为画布的纵向距离）  
    :param rec_lst: 权重列表  
    :return: None
    '''    # Check the total area of rectangles equals the Canvas's area  
    if abs(dx*dy-sum(rec_lst)) >= 1e-5:  
        raise ValueError("输入矩形的面积和不等于大矩形面积!")  
    # Sort rectangles in reverse order according to their area  
    rec_lst.sort(reverse=True)  
    # Initialise position information for each rectangle  
    rec = []  
    for v in rec_lst:  
        rec.append({"x":x,"y":y,"v":v,"dx":None,"dy":None})  
    # Start arranging rectangles using squarify   
    rec_res = squarify(x,y,dx,dy,rec,[],min(dx,dy),[])  
    # Draw all the rectangles on the canvas  
    display_rec(rec_res,x,y,dx,dy)

width函数：返回当前行已排列的矩形的行宽

1
2
3
4
5
6
7
8
9
10
11
def width(rec_row,w):  
    '''  
    返回当前已经排列矩形所组成的行的宽度  
    计算方式：当前行已排列矩形的面积和/行高  
    :param rec_row: 当前行矩形列表  
    :param w: 行高  
    :return: 返回当前已经排列矩形所组成的行的宽度  
    '''    
    totalS = sum(map(lambda x:x["v"],rec_row))  
    h = totalS/w  
    return h

示意图如下：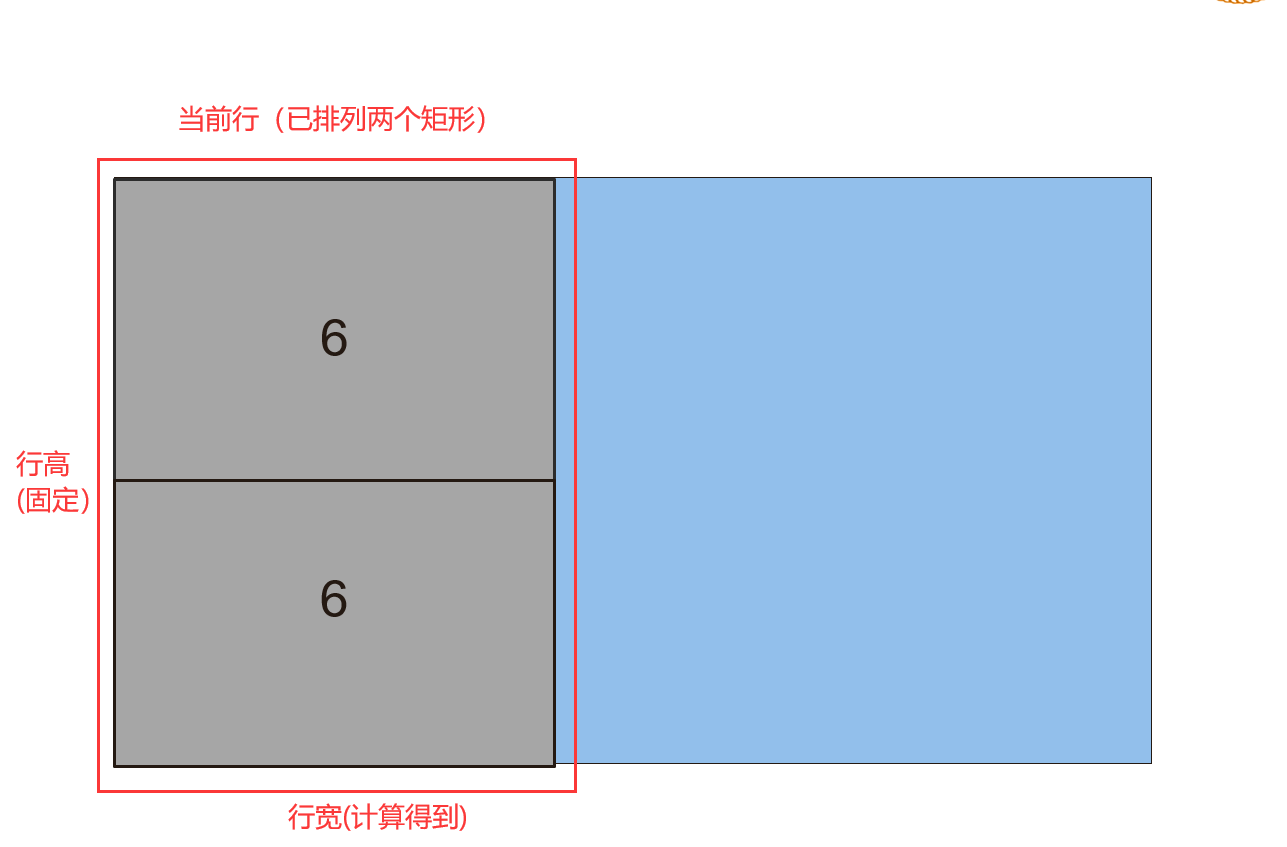

worse函数：返回当前行已排列的矩形中最大的横纵比

1
2
3
4
5
6
7
8
9
10
def worse(res_lst,w):  
    '''  
    计算并返回当前排列的矩形中横纵比最差的矩形的横纵比  
    :param res_lst: 当前排列的矩形列表  
    :param w: 行高  
    :return: 当前排列的矩形中横纵比最差的矩形的横纵比  
    '''    if not res_lst:  
        return 0  
    h = width(res_lst,w)  
    return max(map(lambda x:max(x["v"]/(h*h),(h*h)/x["v"] if x["v"]!=0 else 0),res_lst))

arrange函数：调整当前行已排列矩形的位置（因为有新的矩形插入到当前行了）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def arrange(x, y, rec_row, w, arr_type):  
    '''  
    重排列当前行  
    :param x: 当前行左下角x坐标  
    :param y: 当前行左下角y坐标  
    :param rec_row: 当前行矩形列表  
    :param w: 当前行 行高  
    :param arr_type: 排列方式 纵向=-1 横向1  
    :return: None  
    '''    totalS = sum(map(lambda x: x["v"], rec_row))  
    h = totalS / w  
    s = 0  
    for i in range(len(rec_row)):  
        rec = rec_row[i]  
        # 纵向分割  
        if arr_type == -1:  
            rec["x"] = x  
            rec["y"] = y + s / totalS * w  
            rec["dy"] = rec["v"] / h  
            rec["dx"] = h  
            s += rec["v"]  
        # 横向分割  
        elif arr_type == 1:  
            rec["x"] = x + s / totalS * w  
            rec["y"] = y  
            rec["dx"] = rec["v"] / h  
            rec["dy"] = h  
            s += rec["v"]

squarify函数：是布局算法的核心函数，用来递归排列所有子矩形。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
def squarify(x, y, dx, dy, rec_lst, rec_row, w, path):  
    '''  
    递归排列所有子矩形  
    :param x: 当前画布左下角x坐标  
    :param y: 当前画布左下角y坐标  
    :param dx: 当前画布横向距离  
    :param dy: 当前画布纵向距离  
    :param rec_lst: 剩余矩形列表  
    :param rec_row: 当前行矩形列表  
    :param w: 当前行 行高  
    :param path: 存储已排列矩形  
    :return: 返回排列结果即path  
    '''    if not rec_lst:  
        if rec_row:  
            path.extend(rec_row)  
        for rec in path:  
            print(rec)  
        return path[:]  
    rec = rec_lst[0]  
    # 添加到当前行  
    choice1 = worse(rec_row + [rec], w)  
    # 另开一行  
    choice2 = worse(rec_row, w)  
    # 决策一：选择添加到当前行(当前行为空是特例,直接添加)  
    if choice1 <= choice2 or not rec_row:  
        rec_row.append(rec)  
        arrange(x, y, rec_row, w, -1 if dx >= dy else 1)  
        return squarify(x, y, dx, dy, rec_lst[1:], rec_row, w, path)  
  
    # 决策二：另开一行  
    else:  
        path.extend(rec_row)  
        # 当前行纵向排列  
        if dx >= dy:  
            h = width(rec_row, w)  
            x += h  
            dx -= h  
            return squarify(x, y, dx, dy, rec_lst, [], min(dx, dy), path)  
        # 当前行横向排列  
        else:  
            h = width(rec_row, w)  
            y += h  
            dy -= h  
            return squarify(x, y, dx, dy, rec_lst, [], min(dx, dy), path)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def display_rec(rec_lst,x=0,y=0,dx=1,dy=1):  
    '''  
    绘图函数，可视化矩形  
    矩形权重越大，颜色越深    
    :param rec_lst: 矩形列表  
    :param x: 画布左下角x坐标  
    :param y: 画布左下角y坐标  
    :param dx: 画布横向距离  
    :param dy: 画布纵向距离  
    :return:  
    '''    rec_lst = sorted(rec_lst,key=lambda x:x["v"],reverse=True)  
    fig, ax = plt.subplots()  
    pre_s = None  
    sort_i = 0  
    len_s = len(set(map(lambda x:x["v"],rec_lst)))  
    for rectangle in rec_lst:  
        _x = rectangle['x']  
        _y = rectangle['y']  
        _dx = rectangle['dx']  
        _dy = rectangle['dy']  
        _v = rectangle['v']  
        if pre_s==None:  
            pre_s=_v  
        if pre_s!=_v:  
            sort_i += 1  
            pre_s=_v  
        rect = Rectangle((_x, _y), _dx, _dy, edgecolor='black', facecolor=(127/255,127/255,127/255,1-(1/len_s*sort_i)),linewidth = 2)  
        ax.add_patch(rect)  
        ax.text(_x+_dx/2, _y+_dy/2, _v, ha='center', va='center',fontsize=14)  
    ax.set_xlim(x, dx)  
    ax.set_ylim(y, dy)  
    plt.show()

2.2实现效果

样例一

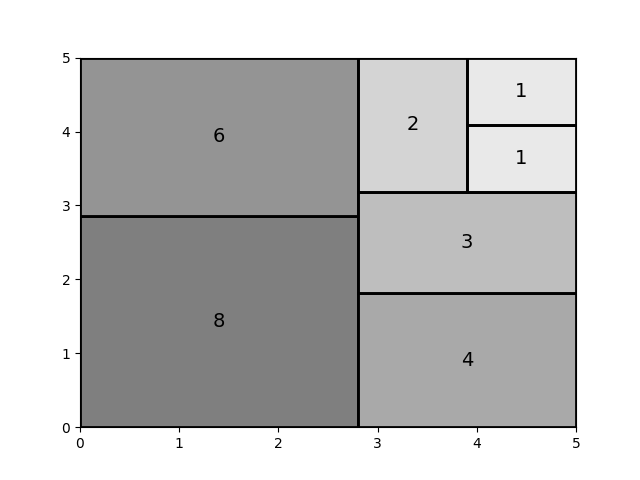
输入：$[6,6,4,3,2,2,1]$

效果如下：这和论文中的例子是一致的，其中权重为1的矩形横纵比较差

样例二

输入：$[8,6,4,3,2,1,1]$

效果如下：细长条略有改善

3.Squarified treemaps优化

3.1 使用Squarified treemaps++优化

优化策略

在原先Squarified treemaps方法中，当前行的排列方式(纵向排列/横向排列)是在当前行的第一个矩形被放置的时候确定的。一般认为如果画布的横向距离dx大于纵向距离dy，采用纵向排列结果更好(因为这样可以使得剩下的画布的横纵比更接近1)，反之采用横向排列。但当后来有新矩形添加到当前行中时，由于需要重新排列，个别矩形的横纵比可能变差。
因此，每当有新矩形加入到当前行，不再保持原先的排列方式不变，而是选用能使得当前行横向比更低的方式。
举例：在权重为3的新矩形未添加到当前行中时，当前行仅有一个权重为4的矩形，且采用横向排列(因为此时画布的dy大于dx）。之后权重为3的新矩形添加到当前行，如果仍然保持横向排列，则该矩形的横纵比较差，但将当前行的排列方式修改为纵向排列，则整体的横纵比得到改进！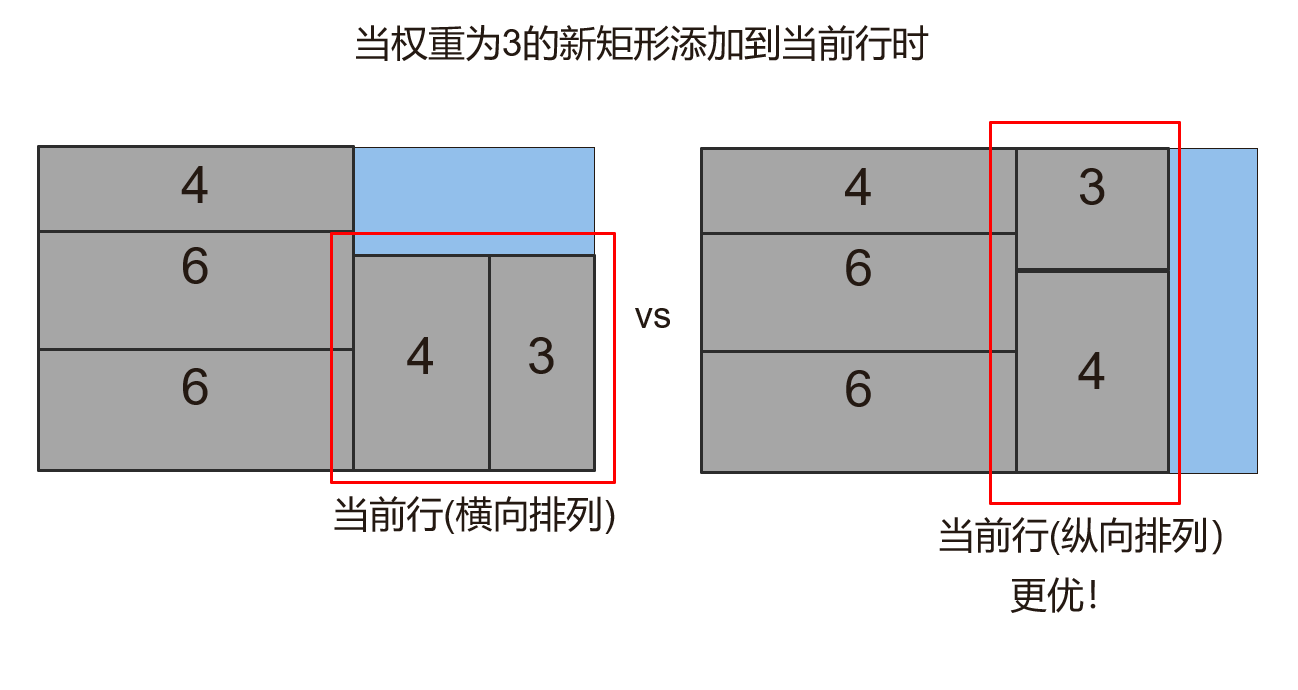

基于上述优化策略的Squarified treemaps++算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
def squarifyPlus(x,y,dx,dy,rec_lst,rec_row,w,path):  
    '''  
    递归排列所有子矩形  
    :param x: 当前画布左下角x坐标  
    :param y: 当前画布左下角y坐标  
    :param dx: 当前画布横向距离  
    :param dy: 当前画布纵向距离  
    :param rec_lst: 剩余矩形列表  
    :param rec_row: 当前行矩形列表  
    :param w: 当前行 行高  
    :param path: 存储已排列矩形  
    :return: 返回排列结果即path  
    '''    
    if not rec_lst:  
        if rec_row:  
            path.extend(rec_row)  
        for rec in path:  
            print(rec)  
        return path[:]  
    rec = rec_lst[0]  
    #添加到当前行  
    choice1 = worse(rec_row+[rec],w)  
    #另开一行  
    choice2 = worse(rec_row,w)  
  
    #选择添加到当前行(当前行为空时,直接添加)  
    if choice1 <= choice2 or not rec_row:  
        rec_row.append(rec)  
        arrange(x,y,rec_row,w,-1 if dx>=dy else 1)  
        return squarifyPlus(x,y,dx,dy,rec_lst[1:],rec_row,w,path)  
    #另开一行  
    else:  
        choice3 = worse(rec_row,dx*dy/w)  
        #原先的分割方式  
        split_type = -1 if dx>=dy else 1  
        if choice3 < choice2:  
            #翻转  
            arrange(x, y, rec_row, dx*dy/w, 1 if dx >= dy else -1)  
            split_type *= -1  
            w = dx*dy/w  
        path.extend(rec_row)  
        #纵向分割  
        if split_type == -1:  
            h = width(rec_row,w)  
            x += h  
            dx -= h  
            return squarifyPlus(x,y,dx,dy,rec_lst,[],min(dx,dy),path)  
        #横向分割  
        elif split_type == 1:  
            h = width(rec_row,w)  
            y += h  
            dy -= h  
            return squarifyPlus(x,y,dx,dy,rec_lst,[],min(dx,dy),path)

优化效果

输入：$[6,6,4,3,2,2,1]$

优化前：其中具有最差横纵比的矩形为权重1的矩形横纵比为3/1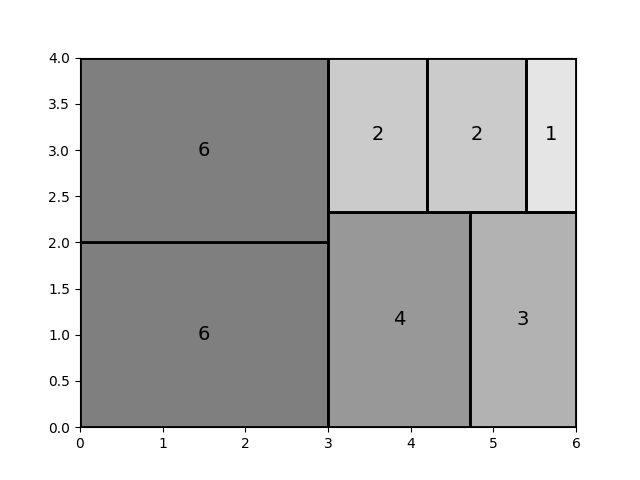

优化后：其中具有最差横纵比的矩形为权重1的矩形横纵比为25/16，比原先3/1改进很多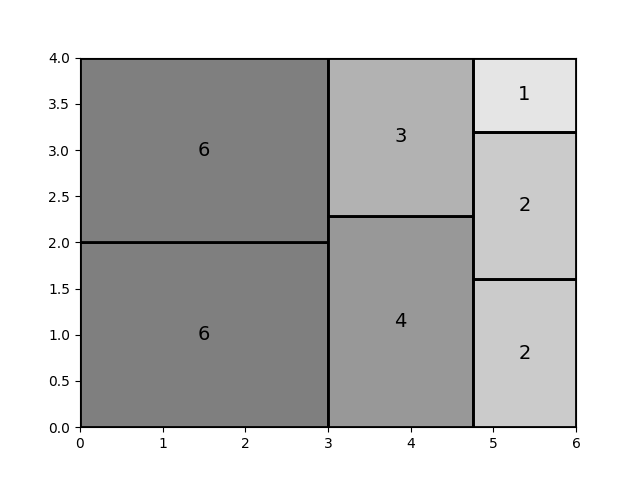

输入：$[10,6,4,3,2,2,1]$

优化前：其中具有最差横纵比的矩形为权重1的矩形横纵比为4/1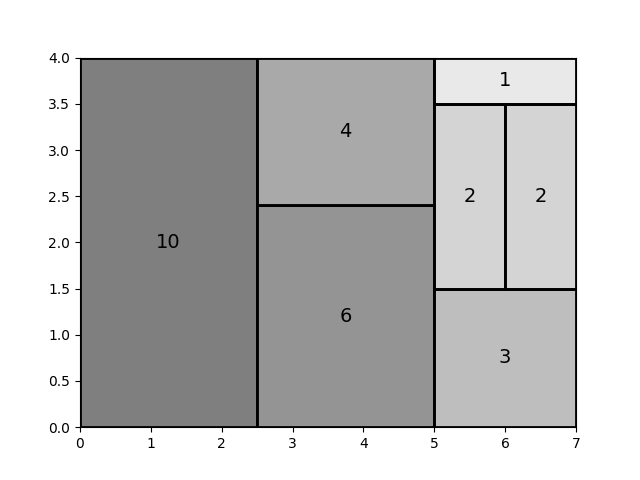

优化后：其中具有最差横纵比的矩形为权重1的矩形横纵比为2.847，有所改进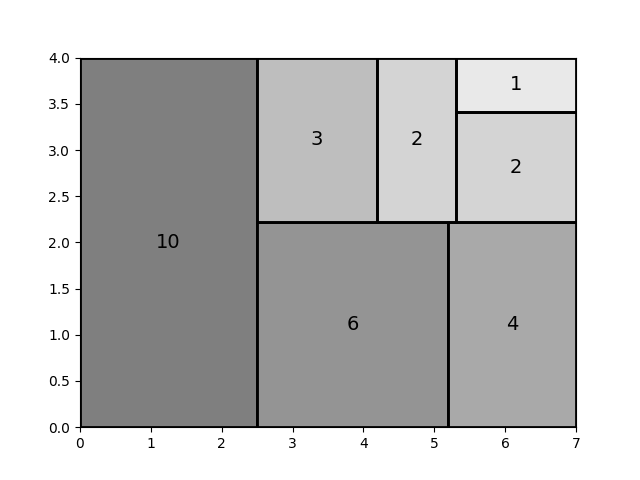

3.2 实现Nested Tree-Map层次关系

实现原理

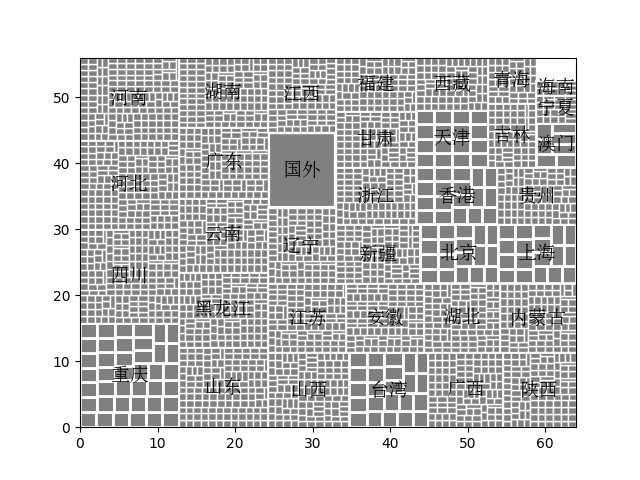
基于上述方式实现的Squarified treemaps无法体现树之间的层次关系以及子节点和父节点之间的联系，仅可作为布局化算法的一种实现。需要呈现层次关系，则需要在算法中添加更多的细节，以及在可视化算法中通过颜色、边框、阴影呈现节点和节点之间的关系。
于是一种可能的改进思路如下，对拥有同一父节点的所有节点进行Squarified treemaps过程，并记录其深度。然后对于其所有的子节点，再次递归进行上述过程。直至子节点为空，递归结束。
上述过程能够保证具有同样父节点的子节点会被安置在同一块大的矩形区域内，这样在进行可视化时，通过节点的深度作不同的渲染效果，达到层次效果和父子关系的体现。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
def squarifyTree(x,y,dx,dy,node,path,level):  
    '''  
    树型squarify treemap  
    :param x: 当前画布左下角x坐标  
    :param y: 当前画布左下角y坐标  
    :param dx: 当前画布横向距离  
    :param dy: 当前画布纵向距离  
    :param node: 当前节点  
    :param path: 存储节点信息  
    :param level: 当前节点深度  
    :return: None  
    '''    
    if node["children"]:  
        node["children"] = sorted(node["children"],key=lambda x:x["v"],reverse=True)  
        rec_child = []  
        for n in node["children"]:  
            _n = {**n,**{"x": x, "y": y, "dx": None, "dy": None}}  
            rec_child.append(_n)  
        rec_res = squarifyPlus(x,y,dx,dy,rec_child,[],min(dx,dy),[])  
        #添加level值  
        for rec in rec_res:  
            rec["level"]=level  
        #加入结果集  
        path.extend(rec_res)  
        #修改孩子节点  
        for i in range(len(node["children"])):  
            #计算孩子节点的x,y,dx,dy  
            rec_parent = rec_res[i]  
            _n = node["children"][i]  
            if not _n["children"]:  
                rec_parent["is_leaf"] = True  
            _v = rec_parent["v"]  
            _x = rec_parent["x"]  
            _y = rec_parent["y"]  
            _dx = rec_parent["dx"]  
            _dy = rec_parent["dy"]  
            #递归处理子节点  
            squarifyTree(_x,_y,_dx,_dy,_n,path,level+1) 

  
def treemapTree(x,y,dx,dy,node,display_key,display_con):  
    '''  
    入口函数  
    :param x: 从(x,y)点开始排列(或理解为画布左下角的x坐标)  
    :param y: 从(x,y)点开始排列(或理解为画布左下角的y坐标)  
    :param dx: 总横向距离（或理解为画布的横向距离）  
    :param dy: 总横向距离（或理解为画布的纵向距离）  
    :param node: 根节点  
    :param display_key: 可视化key，可视化节点的key值，可以是权重或地区名，根据不同需求  
    :param display_con: 可视化信息显示条件，可选leaf:仅显示叶节点 root:仅显示根节点  
    :return:  
    '''    
    path = []  
    squarifyTree(x, y, dx, dy, node, path, 0)  
    display_tree(path, x, y, dx, dy,display_key,display_con)

def display_tree(rec_lst,x=0,y=0,dx=1,dy=1,display_key='v',display_con='leaf'):  
    '''  
    树型可视化  
    :param rec_lst: 矩形列表  
    :param x: 画布左下角x坐标  
    :param y: 画布左下角y坐标  
    :param dx: 画布横向距离  
    :param dy: 画布纵向距离  
    :param display_key: 可视化信息的key，可视化节点的key值，可以是权重或地区名根据不同需求  
    :param display_con: 可视化信息显示条件，可选leaf:仅显示叶节点 root:仅显示根节点  
    :return:  
    '''    
    fig, ax = plt.subplots(figsize=(20,12))  
    max_level = max(map(lambda x:x["level"],rec_lst))  
    for rectangle in rec_lst[::-1]:  
        _x = rectangle['x']  
        _y = rectangle['y']  
        _dx = rectangle['dx']  
        _dy = rectangle['dy']  
        _v = rectangle['v']  
        _level = rectangle['level']  
        _is_leaf = rectangle.get('is_leaf')  
        rect = Rectangle((_x, _y), _dx, _dy, edgecolor=(70/255,130/255,180/255) , fill=False,linewidth = (max_level+1-_level))  
        ax.add_patch(rect)  
        if display_con=='leaf':  
            if _is_leaf:  
                ax.text(_x+_dx/2, _y+_dy/2, rectangle.get(display_key,''), ha='center', va='center',fontsize=14,fontname='SimSun')  
        if display_con=='root':  
            if _level == 0:  
                ax.text(_x + _dx / 2, _y + _dy / 2, rectangle.get(display_key, ''), ha='center', va='center', fontsize=14, fontname='SimSun')  
    ax.set_xlim(x, dx)  
    ax.set_ylim(y, dy)  
  
    plt.gca().set_aspect('equal', adjustable='box')  
    plt.savefig("output.png", dpi=100, bbox_inches='tight', pad_inches=0.1, transparent=False)  
    plt.show()

实现效果

输入

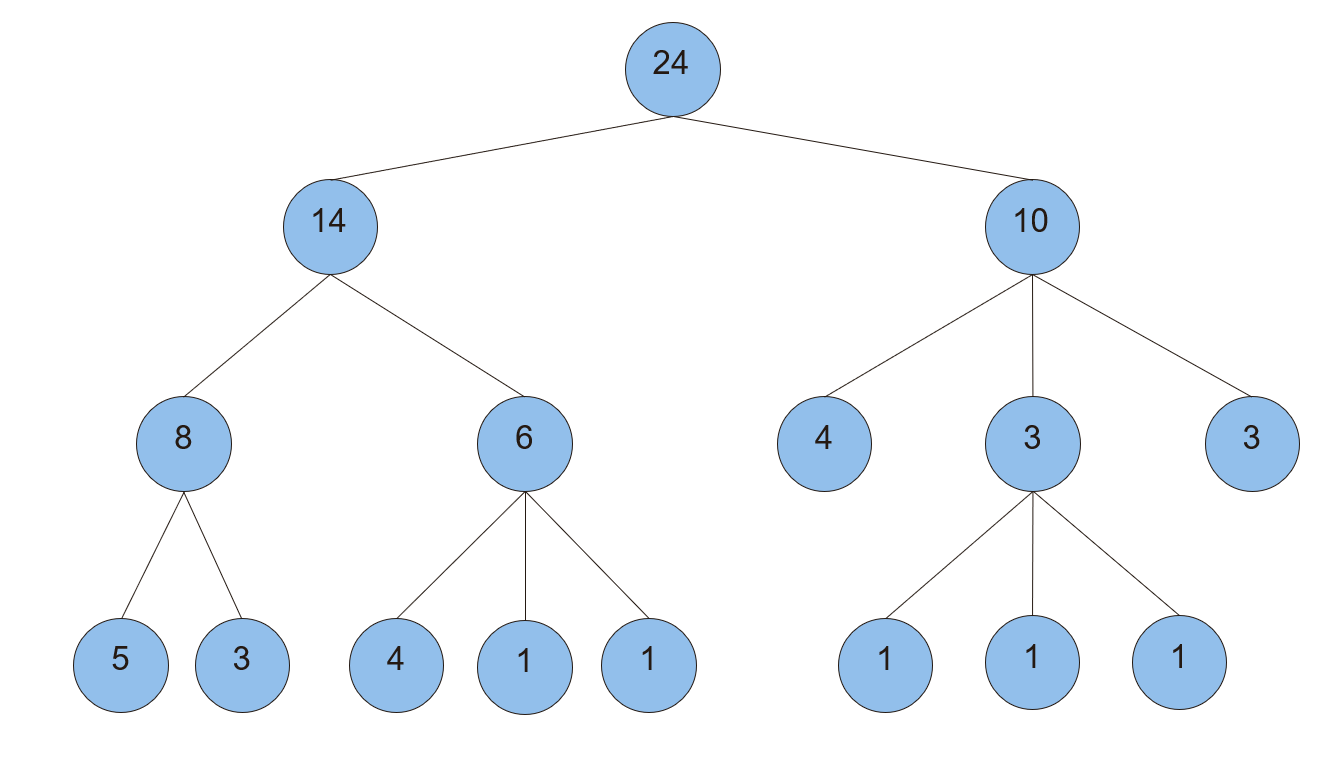
可视化效果

输入China.js中国地区信息，效果如下

总结

评价

  • 改进了[1]中提到的Squarify treemap算法，并增加了颜色透明度变化来体现节点权重大小。
  • 实现的SquarifyPlus和Squarify算法具备复用性，Nested Tree-Map是通过递归调用上述代码实现的。

改进

  • 可视化的效果还可以进一步改进，如：
    • 使用颜色透明度变化，阴影效果改进层次关系。
    • 树型效果不明显，通过边框的粗细来反映层次结构效果略差，未来可进一步使用论文中提及的阴影效果。但Matplotlib可视化库没有相关实现，考虑改用d3.js

参考资料

[1] Bruls, Mark, Kees Huizing, and Jarke J. Van Wijk. “Squarified treemaps.” In Data Visualization 2000, pp. 33-42. Springer, Vienna, 2000.
[2] Balzer, Michael, and Oliver Deussen. “Voronoi treemaps.” In IEEE Symposium on Information Visualization, 2005. INFOVIS 2005., pp. 49-56. IEEE, 2005.

一些失败版本：字体，边框，颜色不合适